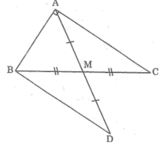
Cho \(\Delta ABC\) có AM là trung tuyến, trên tia đối của tia MA lấy điểm D sao cho MD = MA. Trên BC lấy điểm K sao cho C là trung điểm của BK.
a, Chỉ rõ trọng tâm của tam giác ADK. Vì sao?
b, So sánh các cạnh của tam giác ABC với các trung tuyến của tam giác ADK
c, So sánh các trung tuyến của tam giác ABC với các cạnh của tam giác ADK