ất cả giá trih của x để biểu thức căn -x^2+6x-9 dc xác định
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 2 2023
a: ĐKXĐ: x>=0; x<>1
\(A=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(=\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\)
\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{x-1}=\dfrac{x+\sqrt{x}}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
b: Khi x=9/4 thì A=3/2:1/2=3/2*2=3
28 tháng 4 2023
a: ĐKXĐ: x>=0; x<>1
b \(A=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\)
\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{x\sqrt{x}-1}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{1}{\sqrt{x}+2}\)
c: Khi x=9-4 căn 5 thì \(A=\dfrac{1}{\sqrt{5}-2+2}=\dfrac{\sqrt{5}}{5}\)
d: căn x+2>=2
=>A<=1/2
Dấu = xảy ra khi x=0
25 tháng 12 2023
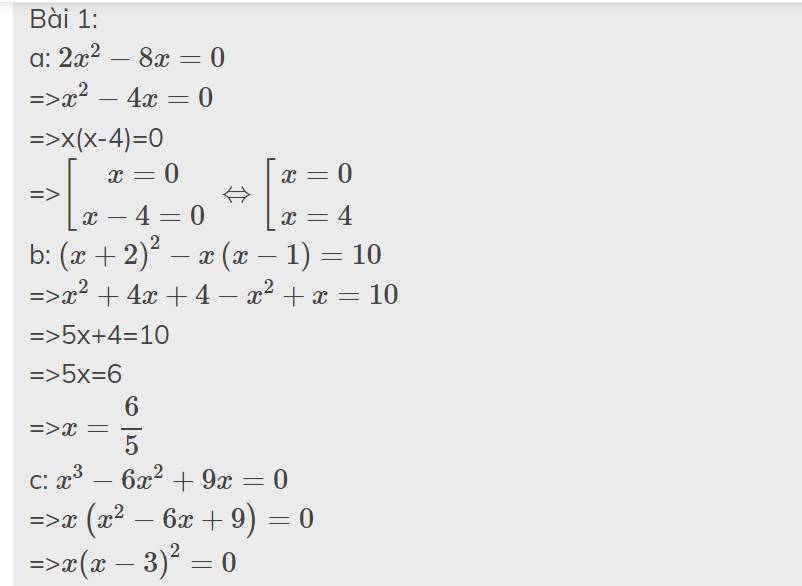
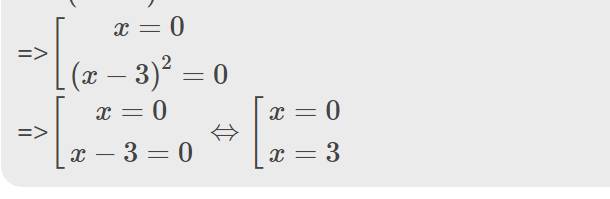Bài 2:
a: ĐKXĐ: \(x\notin\left\{0;-1;\dfrac{1}{2}\right\}\)
b: \(D=\left(\dfrac{x+2}{3x}+\dfrac{2}{x+1}-3\right):\dfrac{2-4x}{x+1}-\dfrac{3x-x^2+1}{3x}\)
\(=\dfrac{\left(x+2\right)\left(x+1\right)+6x-3\cdot3x\left(x+1\right)}{3x\left(x+1\right)}\cdot\dfrac{x+1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{x^2+3x+2+6x-9x^2-9x}{3x}\cdot\dfrac{1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-8x^2+2}{3x}\cdot\dfrac{1}{-4x+2}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-2\left(2x-1\right)\left(2x+1\right)}{3x\cdot\left(-2\right)\left(2x-1\right)}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1}{3x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1+x^2-3x-1}{3x}=\dfrac{x^2-x}{3x}=\dfrac{x-1}{3}\)
c: Khi x=1 thì \(D=\dfrac{1-1}{3}=0\)
21 tháng 12 2023
Bài 1:
a: \(2x^2-8x=0\)
=>\(x^2-4x=0\)
=>x(x-4)=0
=>\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
b: \(\left(x+2\right)^2-x\left(x-1\right)=10\)
=>\(x^2+4x+4-x^2+x=10\)
=>5x+4=10
=>5x=6
=>\(x=\dfrac{6}{5}\)
c: \(x^3-6x^2+9x=0\)
=>\(x\left(x^2-6x+9\right)=0\)
=>\(x\left(x-3\right)^2=0\)
=>\(\left[{}\begin{matrix}x=0\\\left(x-3\right)^2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
6 tháng 1 2023
a: ĐKXĐ: a>=0; a<>4
b: \(M=\dfrac{a\sqrt{a}-a\sqrt{a}+2a-a-2\sqrt{a}}{a-4}=\dfrac{a-2\sqrt{a}}{a-4}=\dfrac{\sqrt{a}}{\sqrt{a}+2}\)
c: Khi a=9 thì \(M=\dfrac{3}{3+2}=\dfrac{3}{5}\)
CM
22 tháng 8 2019
a) x ≠ 0 , x ≠ − 2
b) Ta có D = x 2 - 2x - 2.
c) Chú ý D = - x 2 - 2x - 2 = - ( x + 1 ) 2 - 1 ≤ -1. Từ đó tìm được giá trị lớn nhất của D = -1 khi x = -1.
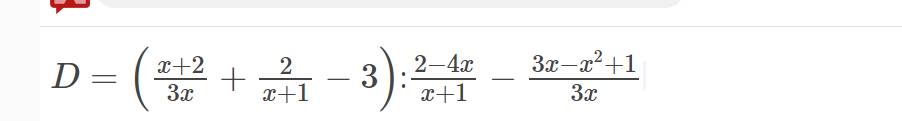
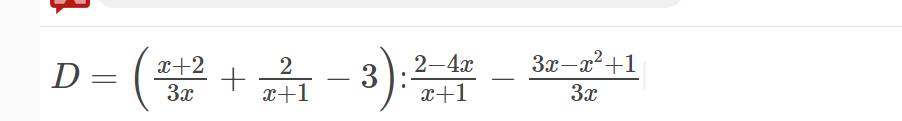
\(\sqrt{-x^2+6x-9}\)
\(\sqrt{-\left(x^2-6x+9\right)}\)
\(\sqrt{-\left(x-3\right)^2}\)
\(\left(x-3\right)^2>=0\)
\(-\left(x-3\right)^2< =0\)
dể biểu thức đc xác định thì \(-\left(x-3\right)^2=0\)
dấu "=" xảy ra khi x=3
kết luận ...............