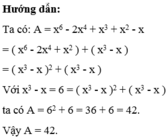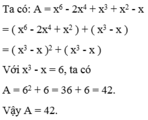Tính giá trị của biểu thức A=x6-2x4+x3+x2-x. Biết x3-x=6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
CM
21 tháng 11 2019
B = x 6 – 2 x 4 + x 3 + x 2 – x ⇔ B = x 6 – x 4 – x 4 + x 3 + x 2 – x ⇔ B = ( x 6 – x 4 ) – ( x 4 – x 2 ) + ( x 3 – x ) ⇔ B = x 3 ( x 3 – x ) – x ( x 3 – x ) + ( x 3 – x ) ⇔ B = ( x 3 – x + 1 ) ( x 3 – x )
Tại x 3 – x = 6, ta có B = (6 + 1).6 = 7.6 = 42
Đáp án cần chọn là: B
PT
1
CM
24 tháng 5 2019
B = x 6 – 2 x 4 + x 3 + x 2 – x ⇔ B = x 6 – x 4 – x 4 + x 3 + x 2 – x ⇔ B = ( x 6 – x 4 ) – ( x 4 – x 2 ) + ( x 3 – x ) ⇔ B = x 3 ( x 3 – x ) – x ( x 3 – x ) + ( x 3 – x ) ⇔ B = ( x 3 – x + 1 ) ( x 3 – x )
Tại x 3 – x = 6, ta có B = (6 + 1).6 = 7.6 = 42
Đáp án cần chọn là: B
8 tháng 8 2021
Ta có: \(x^6-2x^4+x^3+x^2-x\)
\(=x^6-x^4-x^4+x^2+x^3-x\)
\(=x^4\left(x^2-1\right)-x^2\left(x^2-1\right)+\left(x^3-x\right)\)
\(=x^2\left(x^2-1\right)^2+8\)
\(=\left(x^3-x\right)^2+8\)
=72
7 tháng 3 2022
Ta có: \(x^3-2y^2=2^3-2\cdot\left(-2\right)^2=8-8=0\)
Do đó: C=0
NB
7 tháng 3 2022
thay x=2; y=-2 vào \(x^3-2y^2=2^3-2\left(-2\right)^2=8-8=0\)
\(\Rightarrow C=0\)
ko hiểu thì nhìn ở trên các số nhân với nhau nhưng mà lại có 1 thừa số =0 nên cả cái biểu thức =0
T
27 tháng 10 2023
a,
\(A=4(x-2)(x+1)+(2x-4)^2+(x+1)^2\\=[2(x-2)]^2+2\cdot2(x-2)(x+1)+(x+1)^2\\=[2(x-2)+(x+1)]^2\\=(2x-4+x+1)^2\\=(3x-3)^2\)
Thay $x=\dfrac12$ vào $A$, ta được:
\(A=\Bigg(3\cdot\dfrac12-3\Bigg)^2=\Bigg(\dfrac{-3}{2}\Bigg)^2=\dfrac94\)
Vậy $A=\dfrac94$ khi $x=\dfrac12$.
b,
\(B=x^9-x^7-x^6-x^5+x^4+x^3+x^2-1\\=(x^9-1)-(x^7-x^4)-(x^6-x^3)-(x^5-x^2)\\=[(x^3)^3-1]-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1)-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1-x^4-x^3-x^2)\\=(x^3-1)(x^6-x^4-x^2+1)\)
Thay $x=1$ vào $B$, ta được:
\(B=(1^3-1)(1^6-1^4-1^2+1)=0\)
Vậy $B=0$ khi $x=1$.
$Toru$