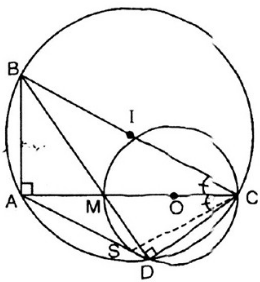
Cho tam giác nhọn ABC. Trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho DA = DC, \(\widehat{ACD}=\frac{1}{2}\widehat{ABC}\)
a. CM tg ABCD nội tiếp
b. Trên đường tròn ngoại tiếp tg ABCD, lấy E,F theo thứ tự là các điểm chính giữa của các cung bị chắn CB, BA bởi các góc CAB, góc BCA. Chứng minh BD vuông góc EF.
c. Gọi M là giao điểm BD và CF. CMR tam giác CDM cân.



Giống bài tập của Nguyễn Thị Lộc