Cho đoạn thẳng AB và CD cắt nhau tại trung điểm O . Gọi E và F lần lượt là trung điểm của AD và BD Gọi I và J lần lượt là giao điểm của CE , CF với AB CMR : AT = Ị = JBCho tam giác ABC có các đường trung tuyến AM, BN, CP cát hau tại G CMR diện tích của 6 tam giác : APG , BPG , BMG,CMG, CNG , ANG = nhauCMR diện tích của ABG = S ( ACG ) = S ( BCG ) Fastest = Winner Nhanh nhất mk tick cho Thời hạn từ h đến 4h...
Đọc tiếp
Cho đoạn thẳng AB và CD cắt nhau tại trung điểm O . Gọi E và F lần lượt là trung điểm của AD và BD Gọi I và J lần lượt là giao điểm của CE , CF với AB
CMR : AT = Ị = JB
Cho tam giác ABC có các đường trung tuyến AM, BN, CP cát hau tại G
CMR diện tích của 6 tam giác : APG , BPG , BMG,CMG, CNG , ANG = nhau
CMR diện tích của ABG = S ( ACG ) = S ( BCG )
Fastest = Winner
Nhanh nhất mk tick cho
Thời hạn từ h đến 4h nhé
❤
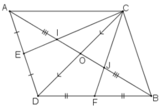
Bài 1 : Tự vẽ hình nha
Đề yêu cầu là cm : AI=IJ=JB ( chứ ko phải AT đâu )
Xét tam giác ADC có : AO và CE là các trung tuyến cắt nhau tại I nên I là trọng tâm tam giác ADC
=> \(AI=\frac{2}{3}AO\) và \(OI=\frac{1}{3}AO\)
Tương tự với tam giác BCD có : J là trọng tâm nên \(BJ=\frac{2}{3}OB\) và \(OJ=\frac{1}{3}OB\)
Mà OA=OB ( gt ) => \(BJ=\frac{2}{3}OA\)
Mặt khác ta có : \(OI+OJ=\frac{1}{3}OA+\frac{1}{3}OB=\frac{1}{3}OA+\frac{1}{3}OA=\frac{2}{3}OA\)
<=> \(IJ=\frac{2}{3}OA\)
Vậy \(AI=IJ=JB=\frac{2}{3}OA\) đpcm
Bài 2 : Ta có \(S_{APG}=S_{BPG}\) ( Vì có chung đỉnh G và hai đáy AP=PB )
\(S_{BMG}=S_{CMG}\) ( Vì có chung đỉnh G và đáy BM=MC )
\(S_{ANG}=S_{CNG}\) ( Vì có chung đỉnh G và hai đáy AN=NC )
Ý 2 :
Vì \(S_{ABM}=\frac{1}{2}S_{ABC}\) ( Vì có chung đỉnh A và đáy BM=1/2 BC )
G là trọng tâm nên AG=2/3 AM => \(S_{ABG}=\frac{2}{3}S_{ABM}=\frac{2}{3}\cdot\frac{1}{2}S_{ABC}=\frac{1}{3}S_{ABC}\)
Làm tương tự ta có : \(S_{ACG}=\frac{1}{3}S_{ABC}\)và \(S_{BGC}=S_{ABC}-S_{ABG}-S_{ACG}=\frac{1}{3}S_{ABC}\)
Vậy S(ABG)=S(ACG)=S(BCG) đpcm