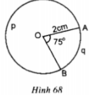
bài 1: cho đường tròn tâm /o bán kính 2cm. Góc SOB =60.
a) tính sđ cung AmB
b) tính độ dài hai cung AnB và AmB, độ dài đường tròn tâm O
c) tính diện tích hình tròn, diện tích hình quạt tròn OAnB.
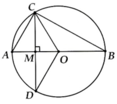
bài 2: cho tam giác ABC có 3 góc nhọn. Đừng tròn tâm O đường kính BC cắt AB, AC lần lượt tại I và K. BK và CI cắt nhua tại H. Tia AH cắt BC tại M.
a) chứng minh \(AM\perp BC\)
b) chứng minh tứ giác BIHM, CMHK, AKMB nội tiếp. xác định tâm đường tròn ngoại tiếp

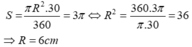
chi oi
ff