cho hình tam giác abc có diện tích 120cm vuông.D là trung điểm của cạnh AC.Trên cạnh AB lấy điểm E sao cho BE= một phần ba BA.Nối B với D và nối C với E.Hai đoạn thẳng BD và CE cắt nhau tại G.Tính diện tích hình tam giác GBC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
14 tháng 12 2020
Xét tg BCE và tg ABC có chung đường cao hạ từ C xuống AB nên
\(\frac{S_{BCE}}{S_{ABC}}=\frac{BE}{BA}=\frac{1}{3}\Rightarrow S_{BCE}=\frac{1}{3}.S_{ABC}\)
\(\Rightarrow S_{ACE}=S_{ABC}-S_{BCE}=S_{ABC}=\frac{1}{3}.S_{ABC}=\frac{2}{3}.S_{ABC}\)
Xét tg CDE và tg ACE có chung đường cao hạ từ E xuống AC nên \(\frac{S_{CDE}}{S_{ACE}}=\frac{CD}{AC}=\frac{1}{2}\Rightarrow S_{CDE}=\frac{1}{2}.S_{ACE}=\frac{1}{2}.\frac{2}{3}.S_{ABC}=\frac{1}{3}.S_{ABC}\)
\(\Rightarrow S_{BCE}=S_{CDE}=\frac{1}{3}.S_{ABC}\) Hai tg này có chung đáy CE nên đường cao hạ từ B xuống CE = đường cao hạ từ D xuống CE
Xét tg BCD và tg ABC có chung đường cao hạ từ B xuống AC nên
\(\frac{S_{BCD}}{S_{ABC}}=\frac{CD}{AC}=\frac{1}{2}\Rightarrow S_{BCD}=\frac{1}{2}.S_{ABC}\)
Xét tg BGC và tg CGD có chung đáy CG và đường cao hạ từ B xuống CE = đường cao hạ từ D xuống CE nên
\(S_{BGC}=S_{CGD}=\frac{1}{2}.S_{BCD}=\frac{1}{2}.\frac{1}{2}.S_{ABC}=\frac{1}{4}.S_{ABC}=\frac{1}{4}.120=30m^2\)
CH
Cô Hoàng Huyền
Admin
VIP
28 tháng 3 2018
Em tham khảo tại đây nhé.
Câu hỏi của Nguyễn Đúc Phương Nam - Toán lớp 5 - Học toán với OnlineMath
20 tháng 7 2015
Ai trả lời giúp mk đi , cả lời giải và phép tính mai mk fai nộp rồi
25 tháng 4 2022
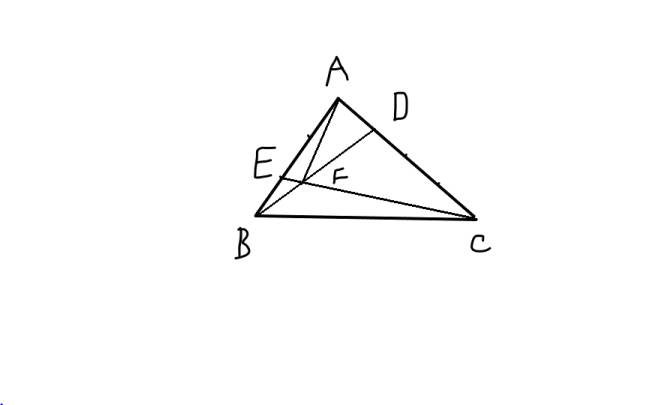Nối A và F , Tam giác EBF và ABF có chung chiều cao hạ từ đỉnh F đáy EB = 1/3 AE
Nên Sebf = 1/3 Sabf , Sbaf : 180 : 1/3 = 540 cm2
Xét hai tam giác AFD và FDC có chung chiều cao hạ từ đỉnh F và đáy AD= 1/3 DC nên Safd = 1/3 Sfdc
Mặt khác hai tam giác này chung đáy FD vậy chiều cao hạ từ đỉnh A bằng 1/3 chiều cao hạ từ đỉnh C
Kéo theo Sfbc= 3 x Afb = 3 x 540 = 1620
Sfbc = 1/3 Sabc
Sabc là : 1620 : 1/3 = 4860 cm2
Ta thấy AE = 2BE nên ta có chiều cao hạ từ A xuống EC bằng 2 lần chiều cao hạ từ B xuống EC.
Từ đó ta có:
\(S_{AGC}=2S_{BGC}\) (Chung cạnh đáy GC)
Lại có tam giác AGD và tam giác GCD có cạnh đáy AD bằng cạnh đáy DC và chung chiều cao hạ từ G xuống AC nên \(S_{AGD}=S_{GCD}\Rightarrow S_{GDC}=\frac{1}{2}S_{AGC}\Rightarrow S_{GDC}=S_{GBC}=\frac{1}{2}S_{BDC}\)
Ta có \(S_{BDC}=\frac{1}{2}S_{ABC}=\frac{1}{2}.120=60\left(cm^2\right)\)
\(\Rightarrow S_{GBC}=60:2=30\left(cm^2\right)\)
cảm ơn bạn nhiều lắm