Tính chu vi của đường tròn ngoại tiếp và diện tích của hình tròn nội tiếp hình vuông có cạnh 20 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NA
0
AD
1
1 tháng 7 2023
S ABCD=36cm2
=>\(AB=\sqrt{36}=6\left(cm\right)\)
\(AC=\sqrt{6^2+6^2}=6\sqrt{2}\left(cm\right)\)
=>\(R=\dfrac{6\sqrt{2}}{2}=3\sqrt{2}\left(cm\right)\)
\(S=R^2\cdot3.14=18\cdot3.14=56.52\left(cm^2\right)\)
13 tháng 4 2017
a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
Hướng dẫn trả lời:
a) Dùng êke ta vẽ hình vuông ABCD có cạnh bằng 4cm như sau:
- Vẽ AB = 4cm.
- Vẽ BC ⊥ AB và BC = 4cm
- Vẽ DC ⊥ BC và DC = 4cm
- Nối D với A, ta có AD ⊥ DC và AD = 4cm
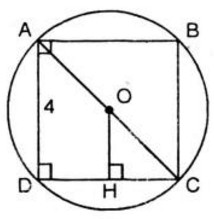
b) Tam giác ABC là tam giác vuông cân nên AB = BC.
Áp dụng định lí Py – ta – go trong tam giác vuông ABC, ta có:
AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=√32=4√2AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=32=42
Vậy AO=R=AC2=4√22=2√2AO=R=AC2=422=22
Vậy R = 2√2 cm
c) Vẽ OH ⊥ Dc. Vẽ đường tròn tâm O, bán kính OH. Đó là đường tròn nội tiếp hình vuông ABCD
Ta có: OH=AD2=2(cm)OH=AD2=2(cm)
Vậy r = OH = 2cm
\
2 tháng 7 2023
AC=căn 2^2+2^2=2*căn 2(cm)
=>R=căn 2(cm)
S1=R^2*3,14=6,28cm2
r=AB/2=1cm
S2=1^2*3,14=3,14cm2
CM
13 tháng 4 2017
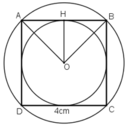
a) Vẽ hình vuông ABCD có cạnh 4cm.
b) Vẽ hai đường chéo AC và BD. Chúng cắt nhau tại O.
Đường tròn (O; OA) là đường tròn ngoại tiếp hình vuông ABCD.
Ta có:
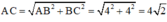(cm)
⇒ R = OA = AC/2 = 2√2 (cm).
c) Gọi H là trung điểm AB.
(O ; OH) là đường tròn nội tiếp hình vuông ABCD.
r = OH = AD/2 = 2cm.
12 tháng 3 2020
Cạnh hình vuông = 9cm
Chu vi hình tròn là 9x3.14=28.26cm
_Kudo_
Bn ơi ! Mk nói này : bn đang hỏi Toán và sao bạn lại cho vào môn là Tiếng Anh.
(với lại mk xin lỗi bn vì mik ko bt làm hihi)
Ta có cạnh của hình vuông là 20 nên theo định lí Pytago ta tính được đường chéo của hình vuông bằng \(\sqrt{20^2+20^2}=20\sqrt{2}\)
và đây cũng chính là độ dài đường kính của đường tròn ngoại tiếp. Nên ta có chu vi đường tròn là \(20\sqrt{2}\pi\approx88,857\)
Ta có đường tròn nội tiếp hình vuông co đương kính bằng cạnh của hình vuông. Nên ta có diện tích hình tròn là\(\frac{20^2}{4}\pi\approx314\)