Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S ABCD=36cm2
=>\(AB=\sqrt{36}=6\left(cm\right)\)
\(AC=\sqrt{6^2+6^2}=6\sqrt{2}\left(cm\right)\)
=>\(R=\dfrac{6\sqrt{2}}{2}=3\sqrt{2}\left(cm\right)\)
\(S=R^2\cdot3.14=18\cdot3.14=56.52\left(cm^2\right)\)

a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
Hướng dẫn trả lời:
a) Dùng êke ta vẽ hình vuông ABCD có cạnh bằng 4cm như sau:
- Vẽ AB = 4cm.
- Vẽ BC ⊥ AB và BC = 4cm
- Vẽ DC ⊥ BC và DC = 4cm
- Nối D với A, ta có AD ⊥ DC và AD = 4cm
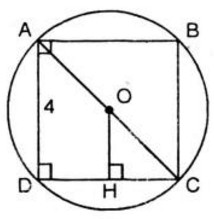
b) Tam giác ABC là tam giác vuông cân nên AB = BC.
Áp dụng định lí Py – ta – go trong tam giác vuông ABC, ta có:
AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=√32=4√2AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=32=42
Vậy AO=R=AC2=4√22=2√2AO=R=AC2=422=22
Vậy R = 2√2 cm
c) Vẽ OH ⊥ Dc. Vẽ đường tròn tâm O, bán kính OH. Đó là đường tròn nội tiếp hình vuông ABCD
Ta có: OH=AD2=2(cm)OH=AD2=2(cm)
Vậy r = OH = 2cm
\

AC=căn 2^2+2^2=2*căn 2(cm)
=>R=căn 2(cm)
S1=R^2*3,14=6,28cm2
r=AB/2=1cm
S2=1^2*3,14=3,14cm2

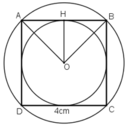
a) Vẽ hình vuông ABCD có cạnh 4cm.
b) Vẽ hai đường chéo AC và BD. Chúng cắt nhau tại O.
Đường tròn (O; OA) là đường tròn ngoại tiếp hình vuông ABCD.
Ta có:
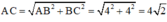 (cm)
(cm)
⇒ R = OA = AC/2 = 2√2 (cm).
c) Gọi H là trung điểm AB.
(O ; OH) là đường tròn nội tiếp hình vuông ABCD.
r = OH = AD/2 = 2cm.

Hình tròn nội tiếp hình vuông có cạnh 4cm thì có R = 2cm.
Vậy diện tích hình tròn là: \(\pi2^2\)=\(4\pi\left(cm^2\right)\)
k cho mk nha