Giả sử hai đường trung tuyến BD và CE của tam giác ABC có độ dài bằng nhau và cắt nhau tại G.
a, tam giác BGC là tam giác gì?
b, so sánh tam giác BCD và tam giác CBE
c, tam giác ABC là tam giác gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 3 2017
a,Ta có: \(BD=CE\Rightarrow\frac{2}{3}BD=\frac{2}{3}CE\Rightarrow BG=CG.\)
Vậy tam giác BCG là tam giác cân tại G.
b, Ta có: \(\hept{\begin{cases}BD=CE\\BG=CG\end{cases}\Rightarrow BD-BG=CE-CG\Rightarrow GD=GE.}\)
Xét \(\Delta BGE\) và \(\Delta CGD:\)
\(\hept{\begin{cases}GD=GE\left(cmt\right)\\\widehat{BGE}=\widehat{CGD}\\BG=CG\left(cmt\right)\end{cases}\Rightarrow\Delta BGE=\Delta CGD\left(c.g.c\right)}\)
\(\Rightarrow BE=CD\)
Xét \(\Delta BCD\) và \(\Delta CDE:\)
\(\hept{\begin{cases}BC:chung\\BE=CD\left(cmt\right)\\BD=CE\left(gt\right)\end{cases}\Rightarrow\Delta BCD=\Delta CDE\left(c.c.c\right)}\)
c, Ta có: \(\Delta BCD=\Delta CDE\left(cmt\right)\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Vậy tam giác ABC là tam giác cân tại A.
1 tháng 5 2023
`@` `\text {dnv}`
`a,`
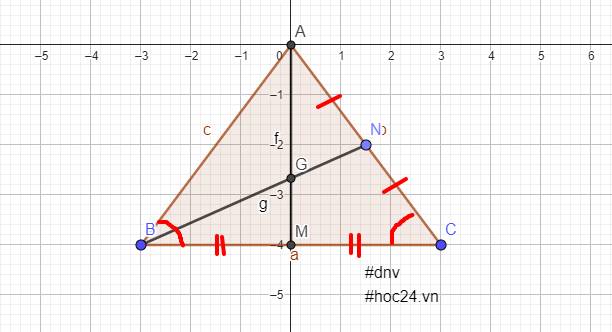
Xét `\Delta AMB` và `\Delta AMC`:
`\text {AB = AC} (\Delta ABC \text {cân tại A})`
`\hat {B} = \hat {C} (\Delta ABC \text {cân tại A})`
`\text {MB = MC (vì AM là đường trung tuyến)`
`=> \Delta AMB = \Delta AMC (c-g-c)`
`b,`
\(\text{Vì AM}\text{ }\cap\text{BN tại G}\)
\(\text{AM, BN đều là đường trung tuyến}\)
`->`\(\text{G là trọng tâm của }\Delta\text{ABC}\)
`@` Theo tính chất của trọng tâm trong tam giác
`->`\(\text{BG = }\dfrac{2}{3}\text{BN}\)
Mà `\text {BN = 15 cm}`
`->`\(\text{BG = }\dfrac{2}{3}\cdot15=\dfrac{15}{3}=5\text{ }\left(\text{cm}\right)\)
Vậy, độ dài của \(\text{BG là 5 cm}\).
`c,` Bạn xem lại đề!
22 tháng 4 2023
a: Xet ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc DEC=góc DBC
c: ΔEBC vuông tại E
mà EO là trung tuyến
nên EO=BC/2
ΔDBC vuông tại D
mà DO là trung tuyến
nên DO=BC/2=EO
=>ΔDOE cân tại O
12 tháng 5 2023
Xét ΔABD và ΔACE có
AB=AC
góc BAD chung
AD=AE
=>ΔABD=ΔACE
Sửa đề: ΔGBC cân tại G
Xét ΔEBC và ΔDCB có
EB=DC
góc EBC=góc DCB
BC chung
=>ΔEBC=ΔDCB
=>góc GBC=góc GCB
=>ΔGBC cân tại G
8 tháng 4 2023
a: Gọi H là trung điểm của AE
=>AH=HE=EB
Xét ΔAEC có AH/AE=AD/AC
nên HD//EC và HD=1/2EC
Xét ΔBHD có BE/BH=BG/BD
nên EG//HD và EG=1/2HD
=>EG=1/4EC
=>EG=1/3GC
\(S_{ABG}=3\cdot S_{GEB}\)(Vì AB=3*BE)
\(S_{GBC}=3\cdot S_{GEB}\)
=>\(S_{ABG}=S_{BGC}\)
b: EG=1/3GC