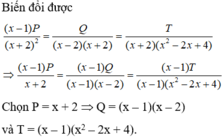
mọi ng ai giải thích giúp mình bước 2 đc ko ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 5 2020
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{132}\)
\(=\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{11\cdot12}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{11}-\frac{1}{12}\)
\(=\frac{1}{1}-\frac{1}{12}\)
\(=\frac{11}{12}\)
29 tháng 5 2020
P/s : chả cần giải thick vì cái này nó sẵn cơ bản rồi.
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{132}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{11.12}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{11}-\frac{1}{12}\)
\(=1-\frac{1}{12}=\frac{11}{12}\)
MH
12 tháng 10 2023
Ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) (tính chất tổng 3 góc trong 1 tam giác)
\(\Rightarrow\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{2}=90^o\)
\(\Rightarrow\dfrac{\widehat{B}+\widehat{C}}{2}=90^o-\dfrac{\widehat{A}}{2}\)
\(\Rightarrow\)\(tan\left(\dfrac{\widehat{B}+\widehat{C}}{2}\right)=tan\left(90^o-\widehat{\dfrac{A}{2}}\right)\)
\(\Rightarrow tan\left(\dfrac{\widehat{B}+\widehat{C}}{2}\right)=cot\dfrac{A}{2}\)
17 tháng 8 2021
Bài 13:
a: Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(AD=DC=\dfrac{AC}{2}\)
mà AB=AC
nên AE=EB=AD=DC
Xét ΔAED có AE=AD
nên ΔADE cân tại A
b: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{BAD}\) chung
AD=AE
Do đó: ΔABD=ΔACE
c: Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà BD=CE
nên BEDC là hình thang cân
TA
0
8 tháng 5 2021
Mây Mamatus ở Việt Nam còn được gọi là mây vảy rồng. Mamatus là 1 thuật ngữ khí tượng học được áp dụng cho hiện tượng nhiễm quang mây treo thành từng lớp dày bên dưới 1 đám mây khác. Nó là hiện tượng khí tượng bình thường. Ở Việt Nam đã nhiều lần xuất hiện những đám mây loại này. Mây Mammatus là một mô hình tế bào của các túi bong bóng treo bên dưới gốc của một đám mây, thường là mây giông vũ tích, mặc dù chúng có thể được gắn vào các lớp khác của đám mây mẹ. Theo bản đồ đám mây quốc tế WMO, mamma là một tính từ bổ sung cho đám mây thay vì là một chi, loài hoặc nhiều đám mây. Chúng được hình thành bởi không khí lạnh chìm xuống để tạo thành túi trái ngược với những đám mây mọc qua sự đối lưu của không khí ấm áp. Bất cứ ai lần đầu tiên nhìn thấy đám mây vảy rồng này cũng đều thốt lên “Bầu trời đang sụp rồi!”. Lạ lùng như vẻ ngoài của chúng, mammatus không nguy hiểm- chúng chỉ đơn giản là báo hiệu rằng một cơn bão có thể ở gần đó.
Khi bạn nhìn thấy những đám mây này là liên quan đến hiện tượng giông bão. Nó thường là mặt dưới của những đám mây đen. Điều kiện đầu tiên hình thành nên những đám mây Mamatus là 1 cơn giông đi kèm với mưa lớn, sấm sét. Tuy nhiên, những đám mây Mamatus này vô hại và sự xuất hiện của nó thường vào giai đoạn tồi tệ nhất khi những cơn giông đi qua. Mamatus bao gồm những tầng mây gợn sóng và được mặt bán trong suốt có thể tạo thành cánh đồng mây trải dài hàng trăm km đều tăm tắp. Một nhóm mây Mamatus có đường kính 1- 3km và dài khoảng 0.5km tồn tại trong khoảng thời gian trung bình từ 1 phút. Tuy nhiên, 1 nhóm mây Mamatus lớn có thể kéo dài từ 15 phút tới vài tiếng đồng hồ. Chúng thường mang theo băng hoặc có thể là giữa băng và nước hoặc chỉ đơn thuần chứa toàn bộ nước trong bụng mây. Mỹ là quốc gia có thể quan sát hiện tượng này nhiều nhất. Trong những tháng thời tiết ấm nóng Mamatus chuyển động của lớp không khí dữ dội nên các nhà khoa học khuyến cáo máy bay không nên hoạt động trong vùng thời tiết nhiều mây này.
Hình ảnh minh hoạ.
8 tháng 11 2021
1) ĐKXĐ: \(x\ge-5\)
\(pt\Leftrightarrow x+5=9\Leftrightarrow x=9-5=4\left(tm\right)\)
2) ĐKXĐ: \(x\ge3\)
\(pt\Leftrightarrow3\sqrt{x-3}-\sqrt{x-3}=6\)
\(\Leftrightarrow2\sqrt{x-3}=6\Leftrightarrow\sqrt{x-3}=3\)
\(\Leftrightarrow x-3=9\Leftrightarrow x=12\left(tm\right)\)
3) ĐKXĐ: \(x\ge-1\)
\(pt\Leftrightarrow\sqrt{\left(x+1\right)^2}-2\sqrt{x+1}=0\)
\(\Leftrightarrow x+1-2\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{x+1}\left(\sqrt{x+1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+1=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\x=3\left(tm\right)\end{matrix}\right.\)
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
`((x-1)P)/(x+2)^2=Q/((x-2)(x+2))=T/((x+2)(x^2-2x+4))`
Nhân 2 vế với `x+2 ne 0` ta có:
`((x-1)P)/(x+2)=Q/(x-2)=T/(x^2-2x+4)`
Nhân cả tử và mẫu với `x-1 ne 0` ta có:
`((x-1)P)/(x+2)=((x-1)Q)/((x-1)(x-2))=((x-1)T)/((x-1)(x^2-2x+4))`