K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 8 2021
Bài 13:
a: Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(AD=DC=\dfrac{AC}{2}\)
mà AB=AC
nên AE=EB=AD=DC
Xét ΔAED có AE=AD
nên ΔADE cân tại A
b: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{BAD}\) chung
AD=AE
Do đó: ΔABD=ΔACE
c: Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà BD=CE
nên BEDC là hình thang cân
8 tháng 8 2023
1:
a: =x^2+3x+4x+12
=x(x+3)+4(x+3)
=(x+3)(x+4)
b: =4x^2-4x-5x+5
=4x(x-1)-5(x-1)
=(x-1)(4x-5)
c: =2x^2-3x-4x+6
=x(2x-3)-2(2x-3)
=(2x-3)(x-2)
3:
a: =2x^2-6xy+xy-3y^2
=2x(x-3y)+y(x-3y)
=(x-3y)(2x+y)
b: =x^2+3xy-xy-3y^2
=x(x+3y)-y(x+3y)
=(x+3y)*(x-y)
c: =6x^2+4xy-3xy-2y^2
=2x(3x+2y)-y(3x+2y)
=(3x+2y)(2x-y)
HN
1
23 tháng 7 2021
11)11) 3x(x-5)2-(x+2)3+2(x-1)3-(2x+1)(4x2-2x+1)=3x(x2-10x+25)-(x3+6x2+12x+8)+2(x3-3x2+3x-1)-(8x3+1)=3x3-30x2+75x-x3-6x2-12x-8+2x3-6x2+6x-2-8x3-1=-4x3-42x2+63x-11
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
23 tháng 8 2021
a: Xét ΔADC có
E là trung điểm của AD
I là trung điểm của AC
Do đó: EI là đường trung bình của ΔADC
Suy ra: EI//DC
Suy ra: EI//DC
Xét hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
b: Ta có: EI//DC
EF//DC
mà EI và EF có điểm chung là E
nên E,I,F thẳng hàng
CC
1
9 tháng 5 2022
Câu 15: (mãi mới nghĩ ra :v)
\(\dfrac{\left(a+b\right)^2}{ab}+\dfrac{\left(b+c\right)^2}{bc}+\dfrac{\left(c+a\right)^2}{ca}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a^2+2ab+b^2}{ab}+\dfrac{b^2+2bc+b^2}{bc}+\dfrac{c^2+2ca+a^2}{ca}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a}{b}+2+\dfrac{b}{a}+\dfrac{b}{c}+2+\dfrac{c}{b}+\dfrac{c}{a}+2+\dfrac{a}{c}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{b}{c}+\dfrac{c}{b}+\dfrac{c}{a}+\dfrac{a}{c}\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow a\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+b\left(\dfrac{1}{c}+\dfrac{1}{a}\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
-Áp dụng BĐT Caushy Schwarz ta có:
\(\left\{{}\begin{matrix}\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{\left(1+1\right)^2}{b+c}=\dfrac{4}{b+c}\\\dfrac{1}{c}+\dfrac{1}{a}\ge\dfrac{\left(1+1\right)^2}{c+a}=\dfrac{4}{c+a}\\\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{\left(1+1\right)^2}{a+b}=\dfrac{4}{a+b}\end{matrix}\right.\)
-Từ đó suy ra: \(a\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+b\left(\dfrac{1}{c}+\dfrac{1}{a}\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge\dfrac{4a}{b+c}+\dfrac{4b}{c+a}+\dfrac{4c}{a+b}\)
-Ta c/m rằng: \(\dfrac{4a}{b+c}+\dfrac{4b}{c+a}+\dfrac{4c}{a+b}\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\ge3\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+1+\dfrac{b}{c+a}+1+\dfrac{c}{a+b}+1-3\right)\ge3\)
\(\Leftrightarrow2\left(\dfrac{a+b+c}{b+c}+\dfrac{b+c+a}{c+a}+\dfrac{c+a+b}{a+b}\right)-6\ge3\)
\(\Leftrightarrow2\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge9\left(1\right)\)
-Áp dụng BĐT Caushy Schwarz cho VT của BĐT ta được:
\(2\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge2\left(a+b+c\right)\left(\dfrac{\left(1+1+1\right)^2}{a+b+b+c+c+a}\right)=2\left(a+b+c\right)\dfrac{9}{2\left(a+b+c\right)}=9\)
\(\Rightarrow\)BĐT (1) đúng.
\(\Rightarrowđpcm\)
-Dấu "=" xảy ra khi \(a=b=c\)
1 tháng 11 2021
Câu 20:
Ta có: \(\widehat{A}-\widehat{B}=40^0\Rightarrow\widehat{B}=\widehat{A}-40^0\)
\(\widehat{A}=2\widehat{C}\Rightarrow\widehat{C}=\frac{\widehat{A}}{2}\)
Vì AB//CD (gt) \(\Rightarrow\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)\(\Rightarrow\widehat{D}=180^0-\widehat{A}\)
Tứ giác ABCD \(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\Rightarrow\widehat{A}+\left(\widehat{A}-40^0\right)+\frac{\widehat{A}}{2}+\left(180^0-\widehat{A}\right)=360^0\)
Và đến đây bạn dễ dàng tìm được góc A và từ đó suy ra được góc D.
1 tháng 11 2021
Câu 29: Ta có:
\(\hept{\begin{cases}xy+x+y=3\\yz+y+z=8\\xz+x+z=15\end{cases}}\Leftrightarrow\hept{\begin{cases}xy+x+y+1=4\\yz+y+z+1=9\\xz+x+z+1=16\end{cases}\Leftrightarrow}\hept{\begin{cases}x\left(y+1\right)+\left(y+1\right)=4\\y\left(z+1\right)+\left(z+1\right)=9\\x\left(z+1\right)+\left(z+1\right)=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=4\\\left(y+1\right)\left(z+1\right)=9\\\left(z+1\right)\left(x+1\right)=16\end{cases}}\)
Đặt \(\hept{\begin{cases}x+1=a\\y+1=b\\z+1=c\end{cases}}\)với a,b,c > 1, khi đó ta có
\(\hept{\begin{cases}ab=4\\bc=9\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}abbc=4.9\\c=\frac{9}{b}\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}16b^2=36\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b^2=\frac{36}{16}=\frac{9}{4}\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{3}{2}\\c=\frac{9}{\frac{3}{2}}=6\\a=\frac{16}{6}=\frac{8}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=a-1=\frac{8}{3}-1=\frac{5}{3}\\y=b-1=\frac{3}{2}-1=\frac{1}{2}\\z=c-1=6-1=5\end{cases}}\)
Vậy \(P=x+y+z=\frac{5}{3}+\frac{1}{2}+5=\frac{10+3+30}{6}=\frac{43}{6}\)
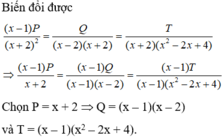
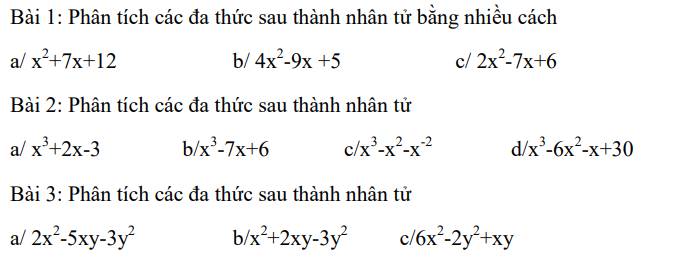
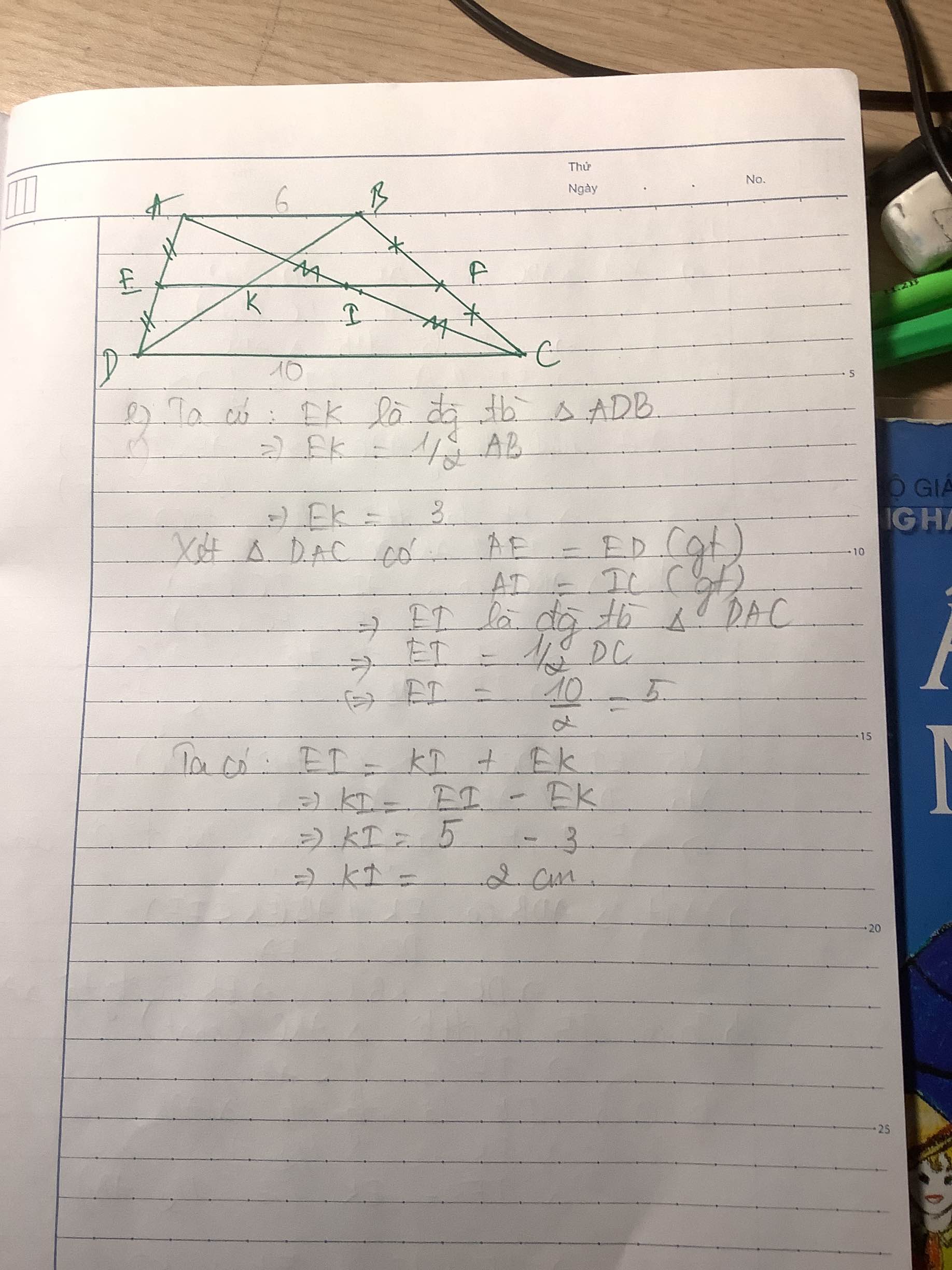
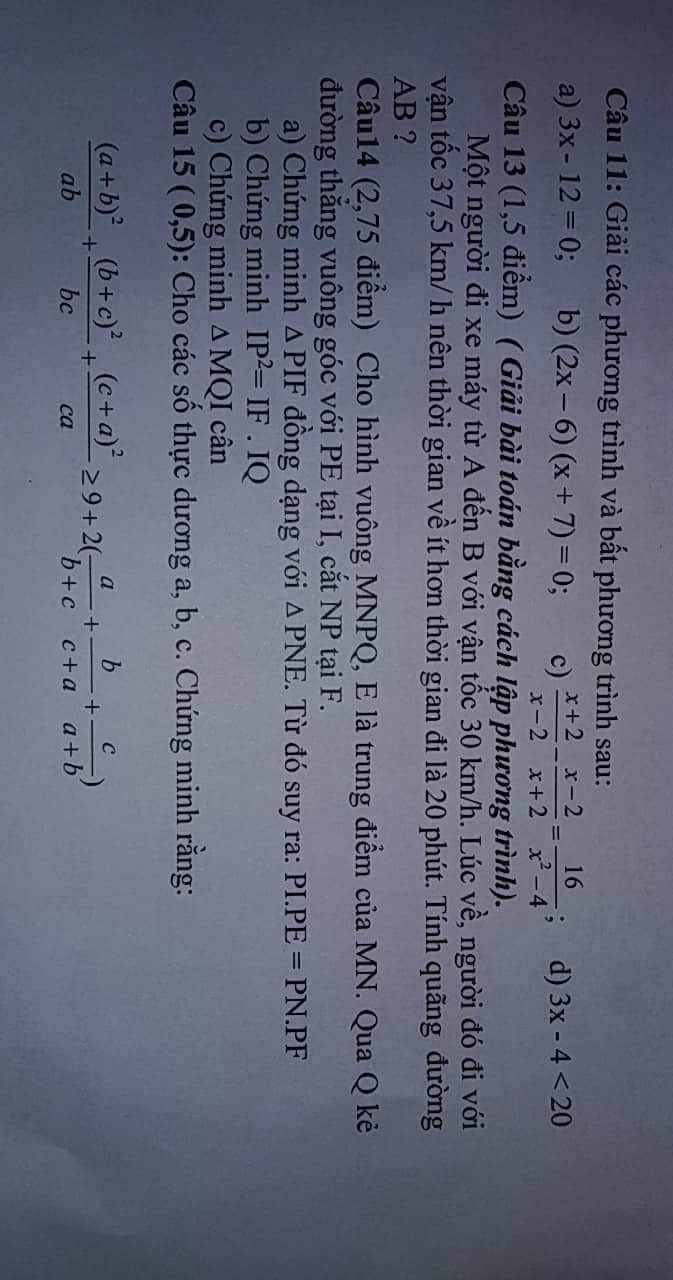
`((x-1)P)/(x+2)^2=Q/((x-2)(x+2))=T/((x+2)(x^2-2x+4))`
Nhân 2 vế với `x+2 ne 0` ta có:
`((x-1)P)/(x+2)=Q/(x-2)=T/(x^2-2x+4)`
Nhân cả tử và mẫu với `x-1 ne 0` ta có:
`((x-1)P)/(x+2)=((x-1)Q)/((x-1)(x-2))=((x-1)T)/((x-1)(x^2-2x+4))`