Cho hàm số y=-3x2 tìm trên đồ thị hàm số 2 điểm A và B sao cho cùng tung độ và khoảng cách AB=12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
17 tháng 2 2021
\(a.\)\(Thay:A\left(2,4\right)\) vào hàm số :
\(\Rightarrow2\cdot4\ne4\)
\(\Rightarrow A\notin y=4x\)
\(b.\\ B\left(x,4\right)\)
\(\Rightarrow4=4x\)
\(\Rightarrow x=1\)
\(B\left(1,4\right)\)
17 tháng 2 2021
a) Thay x=2 vào hàm số y=4x, ta được:
\(y=4\cdot2=8\ne y_A\)
Vậy: Điểm A(2;4) không thuộc đồ thị hàm số
b) Vì điểm B thuộc đồ thị hàm số y=4x và B có tung độ bằng 4 nên Thay y=4 vào hàm số y=4x, ta được:
4x=4
hay x=1
Vậy: B(1;4)
27 tháng 12 2021
a: Thay x=2 và y=-1 vào y=ax, ta được:
2a=-1
hay a=-1/2
29 tháng 12 2020
b) Vì A(xA;yA) có tung độ bằng 6 nên yA=6
Thay y=6 vào hàm số y=3x, ta được:
\(3\cdot x=6\)
hay x=2
Vậy: A(2;6)
c) Gọi điểm có tung độ và hoành độ bằng nhau trên đồ thị hàm số y=3x là B(xB;yB)
nên xB=yB
Thay x=y vào hàm số y=3x, ta được:
y=3y
\(\Leftrightarrow y=0\)
Vậy: Điểm trên đồ thị hàm số y=3x có tung độ và hoành độ bằng nhau có tọa độ là (0;0)
27 tháng 4 2023
\(S=\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{43.46}\\ =1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{43}-\dfrac{1}{46}\\ =1-\dfrac{1}{46}\\ =\dfrac{45}{46}\\ \Rightarrow S< 1\)
10 tháng 1 2022
b: Thay x=2 vào y=-3x, ta được:
\(y=-3\cdot2=-6< >y_A\)
Vậy: A không thuộc đồ thị hàm số y=-3x
c: Thay y=4 vào y=-3x, ta được:
-3x=4
hay y=-4/3
20 tháng 12 2023
a: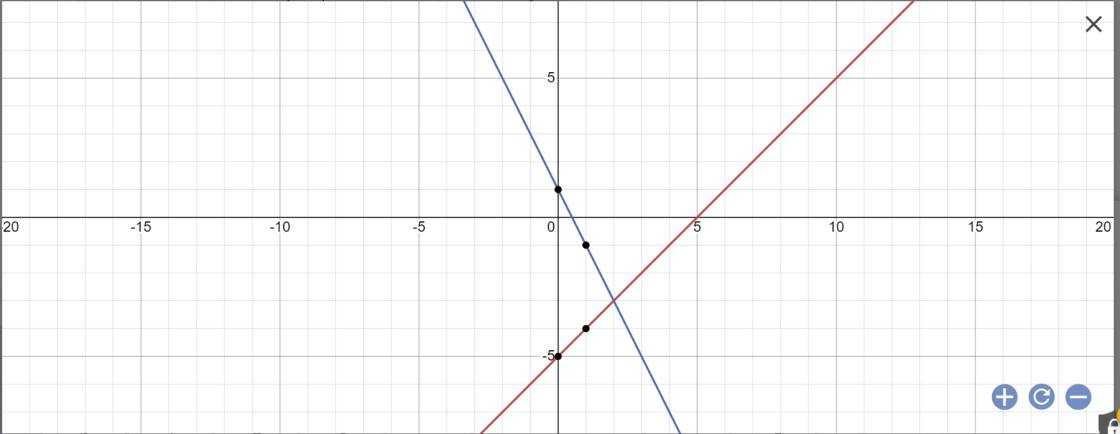 
b: Phương trình hoành độ giao điểm là:
-2x+1=x-5
=>-2x-x=-5-1
=>-3x=-6
=>x=2
Thay x=2 vào y=x-5, ta được:
\(y=2-5=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)
c: (d1): y=x-5
=>x-y-5=0
Khoảng cách từ O(0;0) đến (d1) là:
\(d\left(O;\left(d1\right)\right)=\dfrac{\left|0\cdot1+0\cdot\left(-1\right)-5\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{5}{\sqrt{2}}\)
(d2): y=-2x+1
=>y+2x-1=0
=>2x+y-1=0
Khoảng cách từ O đến (d2) là:
\(d\left(O;\left(d2\right)\right)=\dfrac{\left|0\cdot2+0\cdot1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{5}}\)
toán lớp 3 ko thế đâu