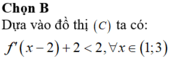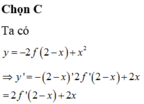cho hàm số : y=x^2; y=-x+2 a, Xác định tọa độ giao điểm A, B của đồ thị 2 hàm số đã cho và tọa độ trung điểm I của đoạn AB, biết rằng A có hoành độ dương b, Xác định tọa độ của điểm M thuộc đồ thị hàm số y=x^2 sao cho tam giác ABM cân tại M
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
1.
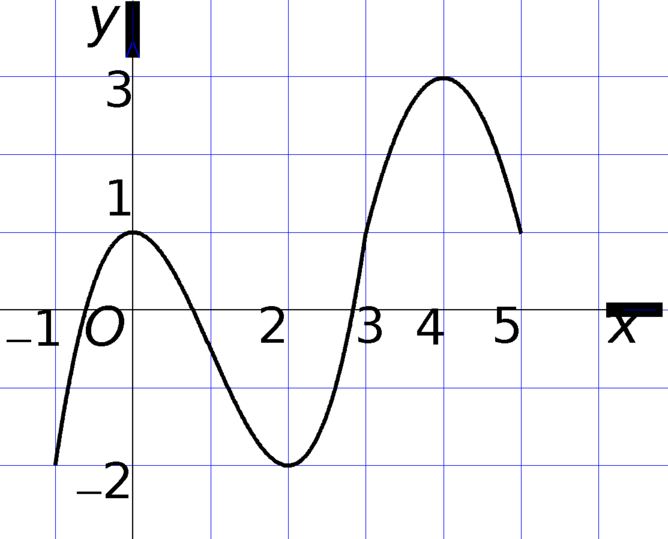
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
23 tháng 11 2021
\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)
15 tháng 8 2023
1:
a: m^2+1>=1>0 với mọi m
=>y=(m^2+1)x-5 luôn là hàm số bậc nhất
b: Do m^2+1>0 với mọi m
nên hàm số y=(m^2+1)x-5 đồng biến trên R
.
.
.
.
CM
10 tháng 8 2019
Chọn C
Ta có 
.
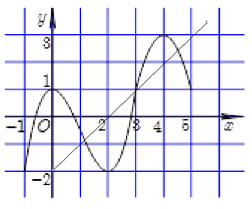
Dựa vào đồ thị ta thấy đường thẳng 
cắt đồ thị 
tại hai điểm có hoành độ nguyên liên tiếp là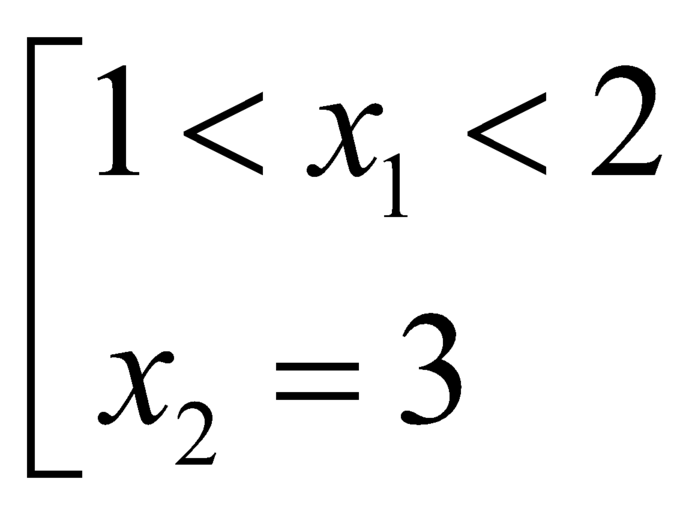 
và cũng từ đồ thị ta thấy 
trên miền 
nên 
trên miền 
.
Vậy hàm số nghịch biến trên khoảng 
.
