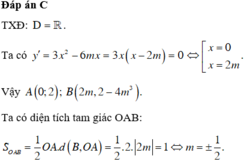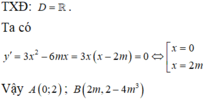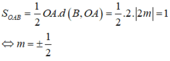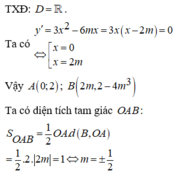Cho hàm số y=x3-3mx2+3.(m2-1)x-m3+4m-1. Tìm m để hàm số có CĐ, CT tại 2 điểm A, B và tam giác OAB vuông tại O (gợi ý \(\overrightarrow{OA}.\overrightarrow{OB}=0\) )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
Đạo hàm y ' = 3 x 2 − 6 m x + 3 m 2 − 1 ; Δ ' = − 3 m 2 − 9 m 2 − 1 = 9 . Suy ra phương trình y ' = 0 có hai nghiệm phân biệt x 1 = 3 m + 3 3 = m + 1 x 2 = 3 m − 3 3 = m − 1
Vậy đồ thị hàm số đã cho luôn có hai điểm cực trị với mọi m.
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là y = − 2 x + 3 m − 1 .
Suy ra tọa độ hai điểm cực trị của đồ thị hàm số đã cho là A m + 1 ; m − 3 và B m − 1 ; m + 1 .
Yêu cầu bài toán ⇔ Δ O A B vuông tại O ⇔ O A → . O B → = 0
⇔ m + 1 m − 1 + m − 3 m + 1 = 0 ⇔ m + 1 2 m − 4 = 0 ⇔ m = − 1 m = 2
Sử dụng MTCT để xác định phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số:
Ta có y ' = 3 x 2 − 6 m x + 3 m 2 − 1 ; y ' ' = 6 x − 6 m . Đưa máy tính về chế độ CMPLX và nhập vào máy biểu thức y − y ' . y ' ' 18 a (coi x = X ; m = Y ).

Ấn ![]() , máy hỏi X? Nhập
, máy hỏi X? Nhập ![]() . Máy hỏi Y? Nhập
. Máy hỏi Y? Nhập![]()
Máy hiện kết quả bằng 299 − 2 i .
Phân tích kết quả: 299 − 2 i = 3.100 − 1 − 2 i = 3 m − 1 − 2 x Suy ra phương trình đường thẳng đi qua hai điểm cực trị là y = − 2 x + 3 m − 1

Chọn B
Có y ' = 3 x 2 − 6 m x + 3 ( m 2 − 1 ) ,
y ' = 0 ⇔ x = m + 1 x = m − 1
Ta có y = y ' ( 1 3 x − m 3 ) − 2 x + 3 m − 1 , vậy đường thẳng qua 2 điểm cực trị là: y = − 2 x + 3 m − 1
2 điểm cực trị của đồ thị là:
A ( m + 1 ; m − 3 ) ; B ( m − 1 ; m + 1 )
Từ giả thiết có:
O A → . O B → = 0 ⇒ m 2 − m − 2 = 0 ⇔ m = − 1 m = 2

\(y'=3x^2-6x-m\)
Hàm số có CĐ, CT khi \(y'=0\) có 2 nghiệm pb
\(\Rightarrow\Delta'=9+3m>0\Rightarrow m>-3\)
Tiến hành chia y cho y' và lấy phần dư ta được phương trình đường thẳng qua CĐ, CT có dạng:
\(y=-\left(\dfrac{2m}{3}+2\right)x-\dfrac{m}{3}+2\)
Do đường thẳng tạo với 2 trục 1 tam giác vuông cân nên có hệ số góc bằng 1 hoặc -1
\(\Rightarrow\left[{}\begin{matrix}-\left(\dfrac{2m}{3}+2\right)=1\\-\left(\dfrac{2m}{3}+2\right)=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{9}{2}< -3\left(loại\right)\\m=-\dfrac{3}{2}\end{matrix}\right.\)