cho nửa đường trong O,đường kính AB =2R.Trên nửa đường tròn này lấy 2 điểm D và E sao cho DE = R (R thuộc cung AE): AD cắt BE tại C.
a) CM; góc CDE=CBA
b) AE cắt BD tại H. chứng minh: CH vuông góc AB
c) tính góc ACB
Giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(Có:\Delta AHO\Omega\Delta ABE\Rightarrow\frac{AH}{AB}=\frac{AO}{AE}\Rightarrow AH.AE=AB.OA\)
\(\Delta BHO\Omega\Delta BAD\left(gg\right)\Rightarrow\frac{BH}{BA}=\frac{BO}{BD}\Rightarrow BH.BD=AB.OB\)
Có : AH.AE + BH.BD = AB.OA + AB.OB = AB . (OA+OB) = AB.AB= AB2 = (2R)2 = 4R2 (đpcm)

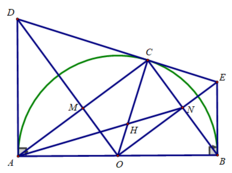
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE
a: A,D,E,B cùng thuộc (O)
=>ADEB là tứ giác nội tiếp
=>\(\widehat{ADE}+\widehat{ABE}=180^0\)
mà \(\widehat{CDE}+\widehat{ADE}=180^0\)(hai góc kề bù)
nên \(\widehat{CDE}=\widehat{CBA}\)
b: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE\(\perp\)CB tại E
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔCAB có
AE,BD là các đường cao
AE cắt BD tại H
Do đó: H là trực tâm của ΔCAB
=>CH\(\perp\)AB
c: Xét (O) có \(\widehat{DHE}\) là góc có đỉnh ở bên trong đường tròn chắn hai cung DE và AB
=>\(\widehat{DHE}=\dfrac{1}{2}\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{DE}\right)\)
\(=\dfrac{1}{2}\left(180^0+60^0\right)=120^0\)
Xét tứ giác CDHE có \(\widehat{CDH}+\widehat{CEH}+\widehat{DCE}+\widehat{DHE}=360^0\)
=>\(\widehat{ACB}+120^0+90^0+90^0=360^0\)
=>\(\widehat{ACB}=60^0\)