Cho tam giác ABC gọi M là trung điểm của AB. Trên tia đối của tia MC lấy điểm N sao cho: MC = MN. Chứng minh rằng:
a, tam giác AMN = tam giác BMC; b, AN song song BC; c, tam giác NAC = tam giác CBN.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ:
a) Vì M là trung điểm của AB nên AM = BM = \(\frac{AB}{2}\)
Xét Δ AMK và Δ BMC có:
AM = BM (cmt)
AMK = BMC (đối đỉnh)
MK = MC (gt)
Do đó, Δ AMK = Δ BMC (c.g.c) (đpcm)
b) Vì N là trung điểm của AC nên AN = NC
Xét Δ ANI và Δ CNB có:
AN = NC (cmt)
ANI = CNB (đối đỉnh)
NI = NB (gt)
Do đó, Δ ANI = Δ CNB (c.g.c)
=> AI = BC (2 cạnh tương ứng) (đpcm)
c) Vì Δ AMK = Δ BMC (câu a) => AKM = MCB (2 góc tương ứng)
Mà AKM và MCB là 2 góc so le trong nên AK // BC (1)
Vì Δ ANI = Δ CNB (câu b) => IAN = NBC (2 góc tương ứng)
Mà IAN và NBC là 2 góc so le trong nên AI // BC (2)
Từ (1) và (2) => AK và AI trùng nhau hay 3 điểm I, A, K thẳng hàng (3)
Có: Δ AMK = Δ BMC (câu a) => AK = BC (2 cạnh tương ứng)
Mà AI = BC (câu b) => AK = AI (4)
Từ (3) và (4) => A là trung điểm của IK (đpcm)

a/ Xét t/g AMD và t/g BMC có
AM = BM (M là TĐ AB)
\(\widehat{AMD}=\widehat{BMC}\) (đối đỉnh) MD = MC (GT)
=> t/g AMD = t/g BMC (c.g.c)
b/ Xets t/g BMD và t/g AMC có
BM = AM
\(\widehat{BMD}=\widehat{AMC}\)(đối đỉnh) MD = MC (GT)
=> t/g BMD = t/g AMC (c.g.c)
=> \(\widehat{ABD}=\widehat{BAC}=90^o\)
=> BD ⊥ AB (1)
c/ Xét t/g BNE và t/g CNA có
BN = CN (N là TĐ BC)
\(\widehat{BNE}=\widehat{CNA}\) (đối đỉnh) NE = NA (GT)
=> T/g BNE = t/g CNA (c.g.c)
=> \(\widehat{EBN}=\widehat{CAB}=90^o\) (2 góc t/ứ)
=> BE ⊥ AB (2) Từ (1) và (2)
=> D , B , E thẳng hàng

a) Vì M1 và M2 là 2 góc đối đỉnh
=>M1 = M2
hay tam giác AMD = tam giác BMC
(Mình ko làm được xin lỗi bạn nha)

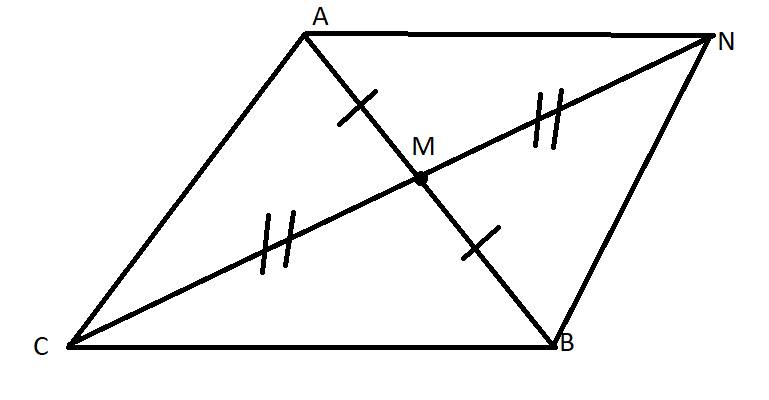
a, Xét ΔAMN và ΔBMC:
AM=BM(M là trung điểm của AB)
MC=MN(GT)
\(\widehat{AMN}=\widehat{BMC}\) (hai góc đối đỉnh)
=>ΔAMN=ΔBMC(c.g.c)
b, ΔAMN=ΔBMC=>\(\widehat{ANM}=\widehat{MCB}\) (2 góc tương ứng) mà 2 góc này nằm ở vị trí so le trong
=>AN//BC
c,+) ΔAMN=ΔBMC =>AN=BC(cạnh tương ứng)
+)Xét ΔAMC và ΔNMB
AM=BM(M là trung điểm của AB)
MC=MN(GT)
\(\widehat{AMC}=\widehat{NMB}\)
=>ΔAMC=ΔNMB(c.g.c)=>AC=BN(cạnh tương ứng)
+)Xét ΔNAC và ΔCBN
AC=BN(CMT)
AN=BC(CMT)
CN là cạnh chung
=>ΔNAC=ΔCBN(c.c.c)

a: Xét tứ giác ABCQ có
N là trung điểm của AC
N là trung điểm của BQ
Do đó: ABCQ là hình bình hành
Suy ra: AQ//BC và AQ=BC
Xét tứ giác ACBP có
M là trung điểm của AB
M là trung điểm của CP
Do đó: ACBP là hình bình hành
Suy ra: AP//BC và AP=BC
Ta có: AQ//BC
AP//BC
mà AQ,AP có điểm chung là A
nên Q,A,P thẳng hàng
mà AP=AQ
nên A là trung điểm của PQ
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
hay MN=PQ/4
=>PQ=4MN

Bạn tham khảo ở đây
Câu hỏi của Công chúa thủy tề - Toán lớp 7 - Học toán với OnlineMath
a) Xét tam giác AMN và tam giác BMC, ta có:
MA = MB (M là trung điểm của AB)
góc NMA = góc BMC (đối đỉnh)
MN = MC (gt)
=> tam giác AMN = tam giác BMC
b) Xét tứ giác ACBN, ta có:
M là trung điểm của AB (gt)
M là trung điểm của CN (MC = MN)
=> Tứ giác ACBN là hình bình hành
=> AN // BC
c) Do tứ giác ACBN là hình bình hành => AN // BC và AN = BC => góc ANC = góc BCN và AN = BC
Xét tam giác NAC và tam giác CBN, ta có:
AN = BC (cmt)
góc ANC = góc BCN (cmt)
CN chung
=> tam giác NAC = tam giác CBN
Vẽ hình đi bạn.