tính a và b biết a - b = a;b = 2( a+b)
Thâth cảm ơn bạn nào giúp mình bài này nhé !!
mk sẽ like đầu tiên người nào nhanh nhất và tất nhiên lm đúng nữa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: a-b=6 => a=b+6
=>a.b = (b+6).b = 16
<=>b2+6b=16
<=>b2+6b-16=0
<=>(b-2).(b+8)=0
<=>\(\left[\begin{array}{nghiempt}b=2\\b=-8\end{array}\right.\)
=>\(\left[\begin{array}{nghiempt}a=8\\a=-2\end{array}\right.\)
=>\(\left[\begin{array}{nghiempt}a+b=10\\a+b=-10\end{array}\right.\)
Bạn xem lại đề bài phần b nhé.
a) Ta có : \(\left(a-b\right)^2=a^2-2ab+b^2=36\Rightarrow a^2+b^2=36+2ab=36+2.16=68\)
Lại có : \(\left(a+b\right)^2=a^2+2ab+b^2=68+2.16=100\Rightarrow a+b=\pm10\)
b) tương tự

+ Chứng minh (a + b)2 = (a – b)2 + 4ab
Ta có:
VP = (a – b)2 + 4ab = a2 – 2ab + b2 + 4ab
= a2 + (4ab – 2ab) + b2
= a2 + 2ab + b2
= (a + b)2 = VT (đpcm)
+ Chứng minh (a – b)2 = (a + b)2 – 4ab
Ta có:
VP = (a + b)2 – 4ab = a2 + 2ab + b2 – 4ab
= a2 + (2ab – 4ab) + b2
= a2 – 2ab + b2
= (a – b)2 = VT (đpcm)
+ Áp dụng, tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4.12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4.3 = 400 + 12 = 412.

a) (a - b)^2 biết a + b =10 và a . b =21
(a - b)^2=a2-2ab+b2=a2+2ab+b2-4ab
=(a+b)2-4ab (1)
thay a + b =10 và a . b =21 vào (1) ta được :
102-4.21
=100-84
=16
vậy (a - b)^2=16 biết a + b =10 và a . b =21
b) (a + b)^2 biết a - b =2 và a . b =-35
(a+b)2=a2+2ab+b2=a2-2ab+b2+4ab
=(a-b)2+4ab (2)
thay a - b =2 và a . b =-35 vào (2) ta được :
22+4.(-35)
=4-140
=-136
vậy (a + b)^2=-136 biết a - b =2 và a . b =-35

\(A^2+B^2=\left(A+B\right)^2-2AB=5\)
\(A^3+B^3=\left(A+B\right)^3-3AB\left(A+B\right)=9\)
\(A^5+B^5=\left(A^2+B^2\right)\left(A^3+B^3\right)-\left(AB\right)^2\left(A+B\right)=5.9-2^2.3=...\)
B.
\(A^2+B^2=\left(A+B\right)^2-2AB=2\)
\(A^6+B^6=\left(A^2\right)^3+\left(B^2\right)^3=\left(A^2+B^2\right)^3-3\left(AB\right)^2\left(A^2+B^2\right)=2^3-3.1^2.2=...\)
Ta có: \(A^2+B^2=\left(A+B\right)^2-2AB=3^2-2.2=5\)
\(A^5+B^5=\left(A^3+B^3\right)\left(A^2+B^2\right)-A^2B^2\left(A+B\right)=\left(A+B\right)\left(A^2-AB+B^2\right)\left(A^2+B^2\right)-A^2B^2\left(A+B\right)=3\left(5-2\right).5-2^2.3=33\)


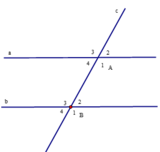
a) Vì B 2 ^ , A 1 ^ là cặp góc trong cùng phía nên ta có:
B 2 ^ + A 1 ^ = 180 0 ⇒ A 1 ^ = 180 0 − B 2 ^ = 180 0 − 45 0 = 135 0 .
b) Ta có B ^ 1 = A ^ 1 = 135 ∘ (hai góc đồng vị)
mà A ^ 3 = A ^ 1 = 135 ∘ (hai góc đối đỉnh)
Vậy B ^ 1 = A ^ 3 = 135 ∘
c) Ta có A ^ 1 + A ^ 2 = 180 ∘ (hai góc kề bù) mà B ^ 1 = A ^ 1 (theo câu b)
Do đó A ^ 2 + B ^ 1 = 180 ∘
Vì a-b=a => b=0.
Ta có:
0=2(a+0)
0:2=a+0
0=a+0
=>a=0.
Vậy a=0, b=0
Tick cho mình nha