Chứng minh rằng, đường thẳng đi qua hai điểm \(A\left( {a;0} \right),B\left( {0;b} \right)\left( {ab \ne 0} \right)\) có phương trình \(\frac{x}{a} + \frac{y}{b} = 1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử có 2 đường thẳng a và a’ đi qua A và vuông góc với d.
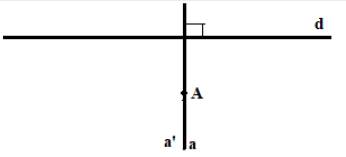
Vì a \( \bot \) d, mà a’ \( \bot \) d nên a // a’ (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Mà A \( \in \) a, A \( \in \) a'
\( \Rightarrow a \equiv a'\)
Vậy có duy nhất đường thẳng đi qua A và vuông góc với d.

a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔABP và ΔAQB có
góc ABP=góc AQB
góc BAP chung
=>ΔABP đồng dạng với ΔAQB
=>AB^2=AP*AQ

Gọi \(M\left( {x;y} \right)\)
Ta có: \(\overrightarrow {AM} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow n = \left( {a;b} \right)\)
\( M \in \Delta \Leftrightarrow \overrightarrow {AM} \bot \overrightarrow n \)
Hay \(\overrightarrow {AM} .\overrightarrow n = 0 \Leftrightarrow a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0\) (ĐPCM).

(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
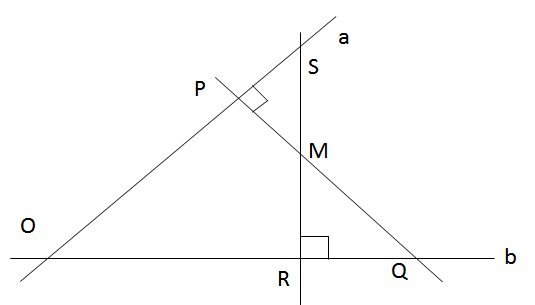
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b

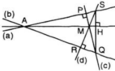
Gọi A là giao điểm của a và b.
Theo giả thiết c ⟘ a hay SR ⟘ AQ hay SR là đường cao của ΔASQ.
d ⟘ b hay PQ ⟘ AS hay QP là đường cao của ΔASQ.
SR cắt QP tại M ⇒ M là trực tâm của ΔASQ
⇒ AM ⟘ SQ
Vậy đường thẳng đi qua M và vuông góc với SQ cũng đi qua A (đpcm).
Đường thẳng AB có một vectơ chỉ phương là \(\overrightarrow {{u_{AB}}} = \overrightarrow {AB} = \left( { - a;b} \right)\). Do đó \(\overrightarrow {{n_{AB}}} = \left( {b;a} \right)\)
Phương trình tổng quát của đường thẳng AB có vectơ pháp tuyến \(\overrightarrow {{n_{AB}}} = \left( {b;a} \right)\) và đi qua điểm \(A\left( {a;0} \right)\)là: \(b\left( {x - a} \right) + a\left( {y - 0} \right) \Leftrightarrow bx + ay - ab = 0 \Leftrightarrow \frac{x}{a} + \frac{y}{b} = 1\).