Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a A B d d' 5cm
Vì \(d\perp a\) tại A
\(d'\perp a\) tại B
=> d // d'
Vậy 2 đường thẳng d, d' không cắt nhau .

Bài làm
d d' a A B 5cm
Vì d vuông góc với a tại A
d' vuông góc với a tại B
=>d // d'
Vậy 2 đường thẳng d và d' không cắt nhau.

A B
Vì 2 dường thẳng d và d' có hai góc trong cùng phía bù nhau nên chúng song song với nhau
Do đó hai đường thẳng d và d' không cắt nhau.

a)tạo với nhau 1 góc bằng 90 độ
b)có mỗi góc bằng 90 độ
c)có 1 và chỉ 1

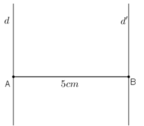
Giả sử đường thẳng d và d’ cắt nhau tại O.
Khi đó qua điểm O ta vẽ được hai đường thẳng phân biệt (d và d’) cùng vuông góc với đường thẳng a (Vô lý).
Vậy đường thẳng d và d’ không cắt nhau.

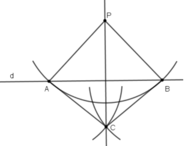
a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
b) Một cách vẽ khác
- Lấy hai điểm A, B bất kì trên d.
- Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
- Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d.
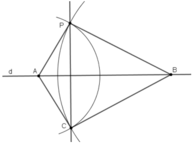
Chứng minh :
- Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
⇒ A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
⇒ B thuộc đường trung trực của PC.
⇒ AB là đường trung trực của PC
⇒ PC ⏊ AB hay PC ⏊ d.

Tiên đề Ơclit được phát biểu như sau : "qua 1 điểm năm ngoài 1 đường thẳng chỉ có 1 đường thẳng song song với đường thẳng đó "
Như vậy , ta thấy phát biểu a) , b) là các phát biểu đúng nội dung tiên đề Ơclit vì đều nói rằng chỉ có 1 đường thẳng qua M và song song với a
a) Đúng
b) Đúng
c) sai
- giải thích : có vô số đường thẳng song song với 1 đường thẳng cho trước
d) sai , nó không thỏa tiên đề Ơ-clit
-giải thích : Qua điểm M nằm ngoài đường thẳng a chỉ có duy nhất và chỉ có 1 đường thẳng song song với a
![]() chúc bạn học tốt !
chúc bạn học tốt !
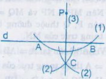
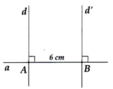
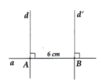
Giả sử có 2 đường thẳng a và a’ đi qua A và vuông góc với d.
Vì a \( \bot \) d, mà a’ \( \bot \) d nên a // a’ (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Mà A \( \in \) a, A \( \in \) a'
\( \Rightarrow a \equiv a'\)
Vậy có duy nhất đường thẳng đi qua A và vuông góc với d.