Bài 1: Cho tam giác ABC có AB=AC, kẻ Ah ⊥ BC tại H.
a) So sánh độ dài hai đoạn thẳng BH và CH;
b) Biết AH = 12cm và BH = 5cm, tính AB;
c) Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho
BD=CE. Kẻ DM ⊥ BC tại M, kẻ En ⊥ BC tại N. Chứng minh BM = CN và tam giác
AMN cân.
Bài 2: Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.
a) Chứng minh △ABH=△ACH . b) Chứng minh AH ⊥ BC.
c) Vẽ HD ⊥ AB (D ∈ AB) và HE ⊥ AC (E ϵ AC) . Chứng minh DE // BC.
Bài 3: Cho tam giác ABC có AB = AC, E là trung điểm BC, trên tia đối của tia EA lấy điểm
D sao cho AE = ED.
a) Chứng minh: △ABE = △DCE. b) Chứng minh: AB // DC.
c) Chứng minh: AE ⊥ BC. d) Tìm điều kiện của △ABC để ∠ADC = 45 độ
Giúp mình vs ạ UwU

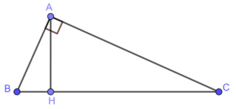
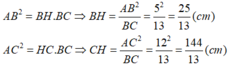
Bài 1:
a) Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH là cạnh chung
Do đó: ΔAHB=ΔAHC(cạnh huyền-cạnh góc vuông)
⇒BH=CH(hai cạnh tương ứng)
b) Áp dụng định lí pytago vào ΔABH vuông tại H, ta được
\(AB^2=AH^2+BH^2\)
hay \(AB=\sqrt{12^2+5^2}=13cm\)
Vậy: AB=13cm
c)
*Chứng minh BM=CN
Ta có: \(\widehat{ABC}=\widehat{MBD}\)(hai góc đối đỉnh)
\(\widehat{ACB}=\widehat{NCE}\)(hai góc đối đỉnh)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{MBD}=\widehat{NCE}\)
Xét ΔMBD vuông tại M và ΔNEC vuông tại N có
BD=CE(gt)
\(\widehat{MBD}=\widehat{NCE}\)(cmt)
Do đó: ΔMBD=ΔNEC(cạnh huyền-góc nhọn)
⇒BM=CN(hai cạnh tương ứng)
*Chứng minh ΔANM cân
Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACN}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
BM=CN(cmt)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
AB=AC(ΔABC cân tại A)
Do đó: ΔABM=ΔACN(c-g-c)
⇒AM=AN(hai cạnh tương ứng)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(định nghĩa tam giác cân)(đpcm)
Bài 2:
a) Xét ΔABH và ΔACH có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}=\widehat{CAH}\)(do AH là tia phân giác của \(\widehat{BAC}\))
AH là cạnh chung
Do đó: ΔABH=ΔACH(c-g-c)
b) Ta có: ΔABH=ΔACH(cmt)
⇒\(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\frac{180^0}{2}=90^0\)
⇒AH⊥BC(đpcm)
c) Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH là cạnh chung
\(\widehat{DAH}=\widehat{EAH}\)(do AH là tia phân giác của \(\widehat{DAE}\))
Do đó: ΔADH=ΔAEH(cạnh huyền-góc nhọn)
⇒AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(định nghĩa tam giác cân)
⇒\(\widehat{ADE}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔADE cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
⇒\(\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{ADE}=\widehat{ABC}\)
mà \(\widehat{ADE}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên DE//BC(dấu hiệu nhận biết hai đường thẳng song song)(đpcm)
Bài 3:
a) Xét ΔABE và ΔDEC có
AE=ED(gt)
\(\widehat{AEB}=\widehat{CED}\)(hai góc đối đỉnh)
BE=EC(do E là trung điểm của BC)
Do đó: ΔABE=ΔDEC(c-g-c)
b) Ta có: ΔABE=ΔDEC(cmt)
⇒\(\widehat{BAE}=\widehat{EDC}\)(hai góc tương ứng)
mà \(\widehat{BAE}\) và \(\widehat{CDE}\) là hai góc ở vị trí so le trong
nên AB//CD(dấu hiệu nhận biết hai đường thẳng song song)
c) Xét ΔAEB và ΔAEC có
AB=AC(ΔABC cân tại A)
AE là cạnh chung
BE=EC(E là trung điểm của BC)
Do đó: ΔAEB=ΔAEC(c-c-c)
⇒\(\widehat{AEB}=\widehat{AEC}\)(hai góc tương ứng)
mà \(\widehat{AEB}+\widehat{AEC}=180^0\)(kề bù)
nên \(\widehat{AEB}=\widehat{AEC}=\frac{180^0}{2}=90^0\)
⇒AE⊥BC(đpcm)
d) Ta có: AB=AC(ΔABC cân tại A)
mà AB=DC(do ΔABE=ΔDEC)
nên AC=DC
Xét ΔACD có AC=DC(cmt)
nên ΔACD cân tại C(định nghĩa tam giác cân)
\(\Rightarrow\widehat{ACD}=180^0-2\cdot\widehat{ADC}\)(số đo của góc ở đỉnh trong ΔACD cân tại C)(1)
Thay \(\widehat{ADC}=45^0\) vào biểu thức (1), ta được
\(\widehat{ACD}=180^0-2\cdot45^0=90^0\)
Ta có: AB//CD(cmt)
\(\Rightarrow\widehat{BAC}+\widehat{ACD}=180^0\)(hai góc trong cùng phía)
hay \(\widehat{BAC}=180^0-\widehat{ACD}=180^0-90^0=90^0\)
Vậy: Khi ΔABC có thêm điều kiện \(\widehat{BAC}=90^0\) thì \(\widehat{ADC}=45^0\)