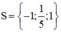Giải các phương trình:
a) 1,2x3 – x2 – 0,2x = 0;
b) 5x3 – x2 – 5x + 1 = 0.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 7 2018
1,2x3 – x2 – 0,2x = 0
⇔ 0,2x.(6x2 – 5x – 1) = 0
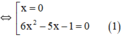
Giải (1): 6x2 – 5x – 1 = 0
có a = 6; b = -5; c = -1
⇒ a + b + c = 0
⇒ (1) có hai nghiệm x1 = 1 và x2 = c/a = -1/6.
Vậy phương trình ban đầu có tập nghiệm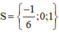 
12 tháng 4 2022
a.\(\left(x^2+2x+5\right)\left(x^2+4x\right)=0\)
Ta có: \(x^2+2x+5=x^2+2x+1+4=\left(x+1\right)^2+4\ge4>0;\forall x\)
\(\Rightarrow x^2+4x=0\)
\(\Leftrightarrow x\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
b.\(\left(x^2-4x+4\right)\left(x^2-3x\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2x\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\\x=3\end{matrix}\right.\)
c.\(1,2x^3-x^2-0,2x=0\)
\(\Leftrightarrow x\left(1,2x^2-x-0,2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-\dfrac{1}{6}\end{matrix}\right.\)
HN
3
DT
16 tháng 2 2022
a/
\(\Leftrightarrow x^2-2x+4-4=0\\ \Leftrightarrow x\left(x-2\right)=0\)
\(\Leftrightarrow x=0;x-2=0\)
\(\Leftrightarrow x=0;x=2\)
DT
16 tháng 2 2022
b/
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)-2x\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3-2x\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3-x\right)=0\)
\(\Rightarrow x=3\)
MH
15 tháng 9 2023
\(a.x^2-4x+4=0\)
\(\left(x-2\right)^2=0\)
=>x=2
b) \(2x^2-x=0\)
\(x\left(2x-1\right)=0\)
=> \(\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
c) \(x^2-5x+6=0\)
\(x^2-2x-3x+6=0\)
\(\left(x-2\right)\left(x-3\right)=0\)
=> \(\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
d) \(x^2+y^2=0\)
Vì \(x^2,y^2\ge0\forall x,y\)
=>x=y=0
e) \(x^2+6x+10=0\)
\(\left(x+3\right)^2+1=0\)
Vì \(\left(x+3\right)^2\ge0\forall x\)
=> VT>0 \(\forall x\)
=> phương trình vô nghiệm
YY
2
10 tháng 2 2022
a, \(x^4-x^2-2=0\Leftrightarrow x^4-2x^2+x^2-2=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(x^2-2\right)=0\Leftrightarrow\left(x^2+1>0\right)\left(x^2-2\right)=0\Leftrightarrow x=\pm\sqrt{2}\)
b, \(\Leftrightarrow x^2\left(x^2+2x+1\right)=0\Leftrightarrow x^2\left(x+1\right)^2=0\Leftrightarrow x=0;x=-1\)
c, \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1>0\right)=0\Leftrightarrow x=1\)
d, \(\Leftrightarrow6x^2-3x-4x+2=0\Leftrightarrow\left(3x-2\right)\left(2x-1\right)=0\Leftrightarrow x=\dfrac{2}{3};x=\dfrac{1}{2}\)
R
10 tháng 2 2022
a)
/ \(x^4+x^2-2=0\)
\(\Leftrightarrow\left(x^2\right)^2-x^2+2x^2-2=0\\ \Leftrightarrow x^2\left(x^2-1\right)+2\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+2=0\\x+1=0\\x-1-0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
HN
1
KK
18 tháng 2 2022
a) (=) x2-2x+4=4 b) (=) 3x-2=0 hoặc 4x+5=0 (=) x2-2x=0 (=) 3x=2 hoặc 4x=5 (=) x(x-2)=0 (=) x=\(\dfrac{2}{3}\) hoặc x=\(\dfrac{5}{4}\) (=) x=0 hoặc x-2=0 (=) x=0 hoặc x=2
D
1
18 tháng 1 2022
\(a.x^2-11x+15=-15.\Leftrightarrow x^2-11x+30=0.\)
\(\Leftrightarrow\left(x-6\right)\left(x-5\right)=0.\Leftrightarrow\left[{}\begin{matrix}x=6.\\x=5.\end{matrix}\right.\)
\(b.2x-3x+10=x.\Leftrightarrow-2x+10=0.\Leftrightarrow x=5.\)
\(c.x^3-4=4.\Leftrightarrow x^3=8.\Leftrightarrow x^3=2^3.\Rightarrow x=2.\)
\(d.x^4+x^3-x^2-x=0.\Leftrightarrow x^2\left(x^2+x\right)-\left(x^2+x\right)=0.\Leftrightarrow\left(x^2-1\right)\left(x^2+x\right)=0.\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)x\left(x+1\right)=0.\Leftrightarrow\left(x-1\right)\left(x+1\right)^2x=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0.\\x+1=0.\\x=0.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1.\\x=-1.\\x=0.\end{matrix}\right.\)
a) 1,2x3 – x2 – 0,2x = 0
⇔ 0,2x.(6x2 – 5x – 1) = 0
Giải (1): 6x2 – 5x – 1 = 0
có a = 6; b = -5; c = -1
⇒ a + b + c = 0
⇒ (1) có hai nghiệm x1 = 1 và x2 = c/a = -1/6.
Vậy phương trình ban đầu có tập nghiệm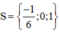
b) 5x3 – x2 – 5x + 1 = 0
⇔ x2(5x – 1) – (5x – 1) = 0
⇔ (x2 – 1)(5x – 1) = 0
⇔ (x – 1)(x + 1)(5x – 1) = 0
Vậy phương trình có tập nghiệm