Cho đoạn mạch như hình vẽ.
Biết R1= 3 Ω; R2= 6 Ω, biến trở đang ở giá trị 10 Ω. Hiệu điện thế ở hai đầu đoạn mạch MN là không đổi.
Tính điện trở tương đương của đoạn mạch MN.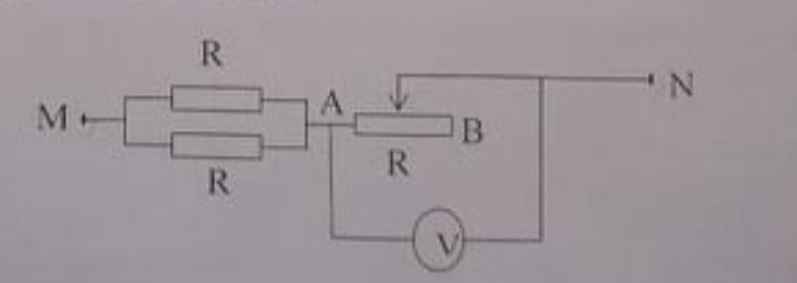
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{6.12}{6+12}=4\left(\Omega\right)\)
\(R_{tđ}=R_1+R_{23}=3+4=7\left(\Omega\right)\)
\(I=I_1=I_{23}=3A\)
\(U_{23}=I_{23}.R_{23}=3.4=12\left(V\right)\)
\(\left\{{}\begin{matrix}I_2=\dfrac{U_2}{R_2}=\dfrac{12}{6}=2\left(A\right)\\I_3=\dfrac{U_3}{R_3}=\dfrac{12}{12}=1\left(A\right)\end{matrix}\right.\)
\(Q_{tỏa}=A=P.t=I^2.R.t=3^2.7.10.60=37800\left(J\right)\)

a) \(R_{12}=R_1+R_2=1+2=3\left(\Omega\right)\)
\(R_{tđ}=\dfrac{R_{12}.R_3}{R_{12}+R_3}=\dfrac{3.3}{3+3}=1,5\left(\Omega\right)\)
b) \(U=U_{12}=U_3=6V\)
\(I_{12}=I_1=I_2=\dfrac{U_{12}}{R_{12}}=\dfrac{6}{3}=2\left(A\right)\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{6}{3}=2\left(A\right)\)
c) \(P=\dfrac{U^2}{R}=\dfrac{6^2}{1,5}=24\left(W\right)\)

\(R_1ntR_2ntR_3\Rightarrow R_{tđ}=R_1+R_2+R_3=10+15+25=50\Omega\)
\(I=I_{AC}=\dfrac{U_{AC}}{R_{AC}}=\dfrac{60}{50}=1,2A\)

Chọn: A
Hướng dẫn:
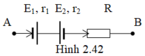
Giả sử dòng điện đi từ A sang B như hình vẽ 2.42 khi đó E 1 là nguồn điện, E 2 là máy thu áp dụng định luật Ôm cho đoạn mạch chứa máy thu:
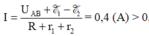
chiều dòng điện đi theo chiều giả sử (chiều từ A sang B).
Thiếu hình vẽ rồi bạn nhé!