Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án C.
Gọi M là trung điểm của BC: 
Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng định lí Pytago vào tam giác ABM ta có:


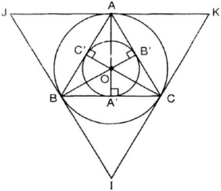
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).
+ Dựng đoạn thẳng AB = 3cm .
+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.
Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.
b) * Vẽ đường tròn:
Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.
Dựng đường trung trực của đoạn thẳng BC và CA.
Hai đường trung trực cắt nhau tại O.
Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.
* Tính bán kính đường tròn.
+ Gọi A’ là trung điểm BC ⇒ A’C = BC/2 = a/2.
và AA’ ⊥ BC
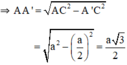
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến
=> Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến
Suy ra O là trọng tâm tam giác ABC.
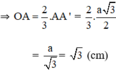
Vậy R = √3 (cm).
c) * Vẽ đường tròn:
Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc 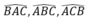
Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.
Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.
* Tính r:
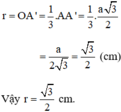
d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).


a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

Chọn đáp án B.
Do O là tâm của đường tròn ngoại tiếp tam giác đều ABC nên O đồng thời là trọng tâm tam giác ABC.
Gọi M là trung điểm BC:


a: góc OAD+góc OBD=180 độ
=>OADB nội tiếp
b: góc OAB+góc OBA=1/2*120=60 độ
=>góc AOB=120 độ
=>góc ADB=60 độ
=>CA=AD=DB=CB
=>CADB là hình thoi


Ta có :
Do BD và CE là các đường cao nên
suy ra góc BEC = góc BDC =90 độ
Xét tứ giác BCDE,có:
góc BEC=góc BDC
vậy BCDE là tứ giác nội tiếp(đpcm)

minh moi bn vao link nay dang ky roi tra loi minigame nha : https://alfazi.edu.vn/question/5b7768199c9d707fe5722878
A B C O D E I
Gọi tiếp điểm của đường tròn (I) với AB và (O;R) theo thứ tự là D và E.
Đường tròn (I) tiếp xúc trong với (O;R) tại E nên 4 điểm A;O;I;E thẳng hàng.
Ta có: AO là phân giác của ^BAC (Do \(\Delta\)ABC đều nội tiếp (O))
=> AI là phân giác ^BAC => ^DAI = ^BAC / 2 = 300
AB tiếp xúc với (I) tại D => ^ADI = 900.
Xét \(\Delta\)AID có: ^ADI = 900; ^DAI = 300 => \(\Delta\)AID nửa đều \(\Rightarrow\frac{ID}{AI}=\frac{1}{2}\)
Hay \(\frac{IE}{AI}=\frac{1}{2}\Rightarrow\frac{IE}{AE}=\frac{1}{3}\)(Do A;I;E thẳng hàng) \(\Rightarrow IE=ID=\frac{2R}{3}\)
Thấy ^ABE chắn nửa đg tròn (O;R) => ^ABE = 900 => BE vuông góc AB. Mà ID vuông góc AB
=> ID // BE => \(\frac{IE}{AE}=\frac{BD}{AB}=\frac{1}{3}\)(Theo ĐL Thales)
Áp dụng ĐL Pytagorean ta dễ dàng tính được: \(AB=R.\sqrt{3}\)\(\Rightarrow BD=\frac{AB}{3}=\frac{R}{\sqrt{3}}\)
Trong \(\Delta\)BDI có ^IDB = 900 . Áp dụng ĐL Pytagorean:
\(IB=\sqrt{BD^2+ID^2}=\sqrt{\frac{R^2}{3}+\frac{4R^2}{9}}=\sqrt{\frac{7R^2}{9}}=\frac{R.\sqrt{7}}{3}\)
ĐS: .....

Bài này khá căn bản thôi do tam giác ABC đều
`=>hatA=hatB=hatC=60^o`
`\hat{BOC}` là góc ở tâm nên gấp 2 lần góc nội tiếp
`=>hat{BOC}=2hatA=120^o`
Vì `hat{OBM}=hat{OCM}=90^o`(do các tt lần lượt lại B,C)
`hat{BOC}+hat{OBM}+hat{OCM}+hat{BMC}=360^o`( đây là tứ giác)
`=>hat{BMC}=360^o-(hat{BOC}+hat{OBM}+hat{OCM}+hat{BMC})=60^o`