Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Chúng ta sẽ dùng cách chứng minh phản chứng
Để ABCD là tứ giác nội tiếp thì OA=OB=OC=OD(O là tâm của đường tròn ngoại tiếp tứ giác nội tiếp ABCD vì O là giao điểm của hai đường chéo)
hay \(OA\cdot OC=OB\cdot OD\)(đpcm)
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Ta có: `hat(ABD) = hat(ACD)`.
Lấy `M in AC` sao cho `hat(ADB) = hat(MDC)`.
`=> triangle ABD ~ triangle MCD`.
`=> (AB)/(MC) = (BD)/(CD) => AB . CD = BD . MC`.
Xét `2 triangle ADM, BDC`, ta có:
`hat(ADM) = hat(BDC)`.
`(DA)/(DM) = (BD)/(DC) ( triangle ABD ~ triangle MCD )`.
`=> triangle ADM ~ triangle BCD => (AD)/(AM) = (BD)/(CB) => AD . BC = BD . AM`
`=> AD . BC + AD . BC = BD . AM + BD . MC`
`=> AD . BC + AD . BC = BD(AM+MC)`
`=> AD.BC+AD.BC = BD . AC => dpcm`.
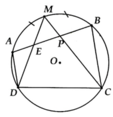
Ta có: A E D ^ = 1 2 s đ A D ⏜ + s đ M B ⏜
= 1 2 s đ D M ⏜ = M C D ^ => D E P ^ + P C D ^ = 180 0
=> PEDC nội tiếp
Chọn đáp án D
(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó )
Phương án A, B, C đúng
bđt ptoleme nhé bạn.
Trên cung nhỏ BC, ta có các góc nội tiếp ∠BAC = ∠BDC, và trên cung AB, ∠ADB = ∠ACB
Gọi M là trung điểm của AC và T là điểm đồng quy của 2 tiếp tuyến tại B, D và đường thẳng AC.
Nhận thấy \(\widehat{OBT}=\widehat{ODT}=\widehat{OMT}=90^o\) nên 5 điểm O, M, B, T, D cùng thuộc đường tròn (OT).
Ta có \(\widehat{DCM}=\widehat{DCA}=\widehat{DBA}\)
Và \(\widehat{DMC}=180^o-\widehat{TMD}\) \(=180^o-\widehat{DBT}\) \(=180^o-\widehat{BCD}\) \(=\widehat{DAB}\)
Nên \(\Delta DAB\sim\Delta DMC\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{MC}=\dfrac{BD}{CD}\)
\(\Rightarrow AB.CD=MC.BD=\dfrac{1}{2}AC.BD\)
Tương tự, ta chứng minh được \(AD.BC=\dfrac{1}{2}AC.BD\) (hoặc cùng có thể dùng định lý Ptolemy trong tứ giác ngoại tiếp để suy ra điều này).
\(\Rightarrow AB.CD=AD.BC\left(=\dfrac{1}{2}AC.BD\right)\)
Ta có đpcm.
Mình trả lời rồi nhé bạn. Nếu bạn chưa xem được đáp án thì bạn vào trang cá nhân của mình xem nhé.