Bài 6 (3 điểm). Cho đường tròn (O;R) có đường kính BC. Lấy A thuộc (O) sao cho AB <AC, vẽ đường cao AH của tam giác ABC.
a) Chứng minh : AH . BC = AB . AC.
b) Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M.
Chứng minh : MA bình phương = MB . MC.
c) Kẻ HE vuông góc AB và HF vuông góc AC . Chứng minh : AM // EF.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOAC cân tại O
mà OD là đường cao
nên OD là phân giác của góc AOC
Xét ΔOAD và ΔOCD có
OA=OC
góc AOD=góc COD
OD chung
Do đó: ΔOAD=ΔOCD
=>góc OCD=90 độ
=>DC là tiếp tuyến của (O)
b: Xét ΔDCE và ΔDBC có
góc DCE=góc DBC
góc CDE chung
Do đó: ΔDCE đồng dạng với ΔDBC
=>DC/DB=DE/DC
=>DC^2=DB*DE

1: \(AO=\sqrt{3^2+8^2}=\sqrt{73}\left(cm\right)\)
BC=2*R=6cm
\(CA=\sqrt{AB^2+BC^2}=\sqrt{8^2+6^2}=10\left(cm\right)\)
BD=6*8/10=4,8cm
2: Xét ΔBCE có
O là trung điểm của BC
OH//CE
=>H là trung điểm của BE
ΔOBE cân tại O
mà OH là trung tuyến
nên OH là phân giác của góc BOE
Xét ΔOBA và ΔOEA có
OB=OE
góc BOA=góc EOA
OA chung
=>ΔOBA=ΔOEA
=>góc OEA=90 độ
=>AE là tiếp tuyến của (O)

a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
Xét ΔBAM vuông tại B có BD là đường cao
nên \(AD\cdot AM=AB^2=4R^2\)

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
TỪ (1) và (2) suy ra OM⊥AB

a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD
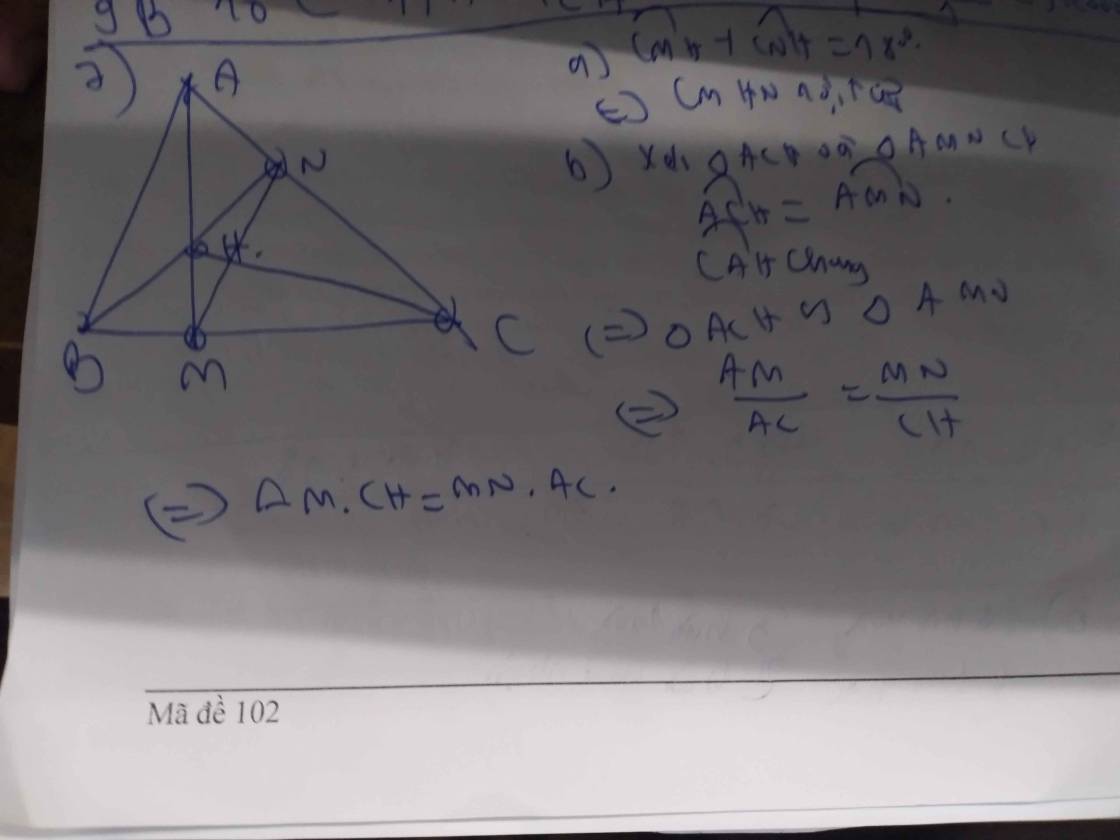
a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
XétΔABC vuông tại A có AH là đường cao
nên \(AH*BC=AB*AC\)