cho Tam giác ABC Gọi I;K lấn lượt là trung điểm của AB và AC,trên tia đối của IC lấy M sao cho I là trung điểm của MC,Trên tia đối của KB lấy N sao cho K là trug điểm của BN
a)CM:AM//BC và AM=BC
b)CM:A là trung điểm của MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DY
18 tháng 1 2023
a,Xét tam giác ABN và tam giác ACM có :
AM=AN (gt)
Góc A chung
AB=AC(gt)
=> tam giác ABN = tam giác ACM (c-g-c)
b,theo câu a =>AMC^=ANB^(1)
Ta có : AM=AN =>tam giác AMN cân tại A => AMN^=ANM^(2)
Từ 1 và 2 =>MNI^=NMI^(3)
Vì B1^=C1^
B^=C^
=>B^-B1^=C-C1^
=>C2^=B2^(4)
Mặt khác : I1^=I2^(đối đỉnh) (5)
Từ 3 ; 4 và 5 => MNI^+NMI^+I1^=180*=I2^+B2^+C2^(tổng 3 góc của 1 tam giác )
=> MNI^+NMI^ / 2 = B2^+C2^ / 2
=> B2^=MNI^
Vì 2 góc này ở vị trí sole trong và bằng nhau
=> MN // BC
CM
27 tháng 12 2019
ΔABC cân tại A
⇒ phân giác AI đồng thời là trung tuyến
⇒ AI đi qua trọng tâm G của ΔABC
Vậy A, I, G thẳng hàng.
TM
21 tháng 1 2022
a. Xét △ABM và △DCM:
\(AM=MD\left(gt\right)\)
\(\hat{AMB}=\hat{DMC}\) (đối đỉnh)
\(BM=MC\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
b. Từ a. => \(\hat{MCD}=\hat{MBA}\) (2 góc tương ứng). Mà hai góc này ở vị trí so le trong
\(\Rightarrow CD\text{ // }AB\left(a\right)\)
c. Xét △CIK và △AIB:
\(AI=IC\left(gt\right)\)
\(\hat{AIB}=\hat{CIK}\) (đối đỉnh)
\(BI=IK\left(gt\right)\)
\(\Rightarrow\Delta CIK=\Delta AIB\left(c.g.c\right)\Rightarrow\hat{ICK}=\hat{IAB}\). Mà hai góc ở vị trí so le trong
\(\Rightarrow AB\text{ // }CK\left(b\right)\)
Từ (a) và (b), theo tiên đề Ơ-clit \(\Rightarrow AB\text{ // }DK\)
Vậy: D, C, K thẳng hàng (đpcm).
21 tháng 1 2022
a) Xét tam giác ABM và tam giác DCM:
BM = CM (M là trung điểm BC).
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh).
MA = MD (cmt).
\(\Rightarrow\) Tam giác ABM = Tam giác DCM (c - g - c).
b) Ta có: \(\widehat{BAM}=\widehat{CDM}\) (Tam giác ABM = Tam giác DCM).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) CD // AB (dhnb).
c) Xét tứ giác AKCB có:
I là trung điểm AC (gt).
I là trung điểm BK (IB = IK).
\(\Rightarrow\) Tứ giác AKCB là hình bình hành (dhnb).
\(\Rightarrow\) CK // AB (Tính chất hình bình hành).
Mà CD // AB (cmt).
\(\Rightarrow\) D, C, K thẳng hàng.
CM
12 tháng 12 2017
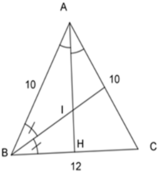
Ta có: AB = AC = 10cm
Suy ra ΔABC cân tại A
Có I là giao các đường phân giác của ΔABC
Suy ra AI, BI là đường phân giác của ΔABC
Gọi H là giao của AI và BC
Khi đó ta có AH vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân ABC (tính chất tam giác cân).
=> H là trung điểm của cạnh BC
=> BH = HC = B C 2 = 12 2 = 6cm
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:
A H 2 + B H 2 = A B 2 ⇔ A H 2 + 6 2 = 10 2 ⇔ A H 2 = 100 – 36 = 64 ⇒ A H = 8
Vì BI là phân giác của tam giác ABH nên: A B B H = A I I H = A H − I H I H
ó 10 6 = 8 − I H I H ó 10IH = 48 – 6IH ó IH = 3
Áp dụng định lý Pitago trong tam giác BHI vuông tại H, ta có:
B I 2 = I H 2 + B H 2 ⇔ B I 2 = 3 2 + 6 2 ⇔ B I 2 = 45 ⇒ B I = 3 5
Đáp án: D
AH
Akai Haruma
Giáo viên
29 tháng 3 2023
Lời giải:
Ta thấy:
$\widehat{BID}=180^0-\widehat{BIA}=\widehat{ABI}+\widehat{BAI}$
$=\frac{\widehat{B}}{2}+\frac{\widehat{A}}{2}=\frac{\widehat{A}+\widehat{B}}{2}$
$=\frac{180^0-\widehat{C}}{2}=90^0-\widehat{C}.\frac{1}{2}$
$=90^0-\widehat{ICH}=\widehat{CIH}$
Vậy:
$\widehat{BID}=\widehat{CIH}$
$\Rightarrow \widehat{BIH}+\widehat{HID}=\widehat{HID}+\widehat{CID}$
$\Rightarrow \widehat{BIH}=\widehat{CID}$ (đpcm)
31 tháng 8 2017
nếu rảnh có thể tham khảo tại
Trường Toán Pitago – Hướng dẫn Giải toán - Học toán lớp 3,4,5,6,7,8,9 - Học toán trên mạng - Học toán online
CM
25 tháng 12 2017
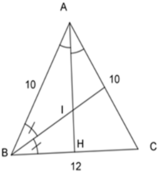
Ta có: AB = AC = 10cm
Suy ra ΔABC cân tại A
Có I là giao các đường phân giác của ΔABC
Suy ra AI, BI là đường phân giác của ΔABC
Gọi H là giao của AI và BC
Khi đó ta có AH vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân ABC (tính chất tam giác cân).
=> H là trung điểm của cạnh BC
=> BH = HC = B C 2 = 12 2 = 6cm
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:
A H 2 + B H 2 = A B 2 ⇔ A H 2 + 6 2 = 10 2 ⇔ A H 2 = 100 – 36 = 64 ⇒ A H = 8
Vì BI là phân giác của tam giác ABH nên: A I I H = A B B H = 10 6 = 5 3
⇔ A I 5 = I H 3
Theo tính chất dãy tỉ số bằng nhau ta có:
A I 5 = I H 3 = A I + I H 5 + 3 = A H 8 = 8 8 = 1
=> AI = 5(cm)
Đáp án: C