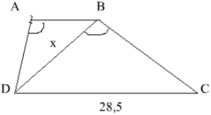
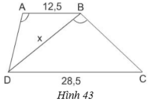
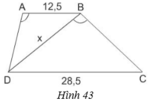
Cho hình thang ABCD (AB//CD) với AB= 12,5cm; CD = 28,5cm;góc DAB bằng góc DBC. Tính độ dài đoạn thẳng BD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét Δ ABD và Δ BDC có:
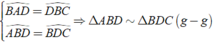
⇒ AB/BD = AD/BC = BD/DC
hay 12,5/x = x/28,5 ⇒ x 2 = 1425/4 ⇔ x ≈ 18,87
Chọn đáp án D.

Chung minh ABD đồng dạng với BDC
=> \(\widehat{ABD}\)=\(\widehat{BDC}\)
hai góc này ở vị trí sole trong
=> AB//CD

a)Vẽ ∆DBC biết BD = 5 cm, BC = 10 cm, DC = 12,5 cm.
Trên nửa mặt phẳng bờ BD không chứa C vẽ hai cung tròn tâm B và tâm D bán kính lần lượt là 4 cm và 8 cm. Hai cung này cắt nhau tại A.
Vẽ các đoạn BA, DA được tứ giác ABCD.
ABBD=410=25;BDDC=1025=25;ADBC=820=25ABBD=410=25;BDDC=1025=25;ADBC=820=25
=>ABBD=BDDC=ADBC=>ΔABDΔBDCABBD=BDDC=ADBC=>ΔABDΔBDC
∆ABD∽ ∆BDC =>ˆABD=ˆBDCABD^=BDC^ lại so le trong.
=>AB // DC hay ABCD là hình thang.

a, Xét ΔABD và ΔBDC có :
\(\widehat{A}=\widehat{DBC}\left(gt\right)\)
\(\widehat{ABD}=\widehat{BDC}\left(AB//CD;slt\right)\)
\(\Rightarrow\Delta ABD\sim\Delta BDC\left(g-g\right)\)
b, Ta có : \(\Delta ABD\sim\Delta BDC\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{BD}=\dfrac{BD}{DC}\)
hay \(BD^2=AB.DC=12.28,5=342\)
\(\Rightarrow BD=\sqrt{342}\left(cm\right)\)