Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

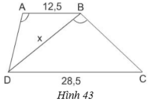
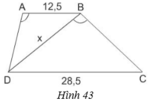
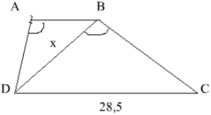
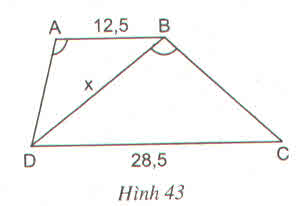
Xét Δ ABD và Δ BDC có:
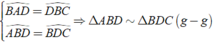
⇒ AB/BD = AD/BC = BD/DC
hay 12,5/x = x/28,5 ⇒ x 2 = 1425/4 ⇔ x ≈ 18,87
Chọn đáp án D.

Xét ∆ABD và ∆BDC có:

=> ∆ABD ∽ ∆BDC(trường hợp 3)

=> BD = √(AB.DC) = √(12,5.8,5) = √356,25 => BD = 18,9 cm

a: Xét ΔABD và ΔBDC có
góc DAB=góc CBD
góc ABD=góc BDC
=>ΔABD đồng dạng với ΔBDC
b: ΔABD đồng dạng ΔBDC
=>BA/BD=BD/DC
=>BD^2=4*9=36
=>BD=6cm
c: ΔABD đồng dạng với ΔBDC
=>\(\dfrac{S_{ABD}}{S_{BDC}}=\left(\dfrac{4}{6}\right)^2=\dfrac{4}{9}\)
=>\(S_{BDC}=32:\dfrac{4}{9}=72\left(cm^2\right)\)

Xét ∆ABD và ∆BDC có:
+) \(\widehat{DAB}\) = \(\widehat{DBC}\) (gt)
+) \(\widehat{ABD}\) = \(\widehat{BDC}\) (Hai góc so le trong)
\(=> ∆ABD ∽ ∆BDC\) (g-g)
=> \(\dfrac{AB}{BD}\) = \(\dfrac{BD}{DC}\) (tính chất hai tam giác đồng dạng)
=> BD2 = AB.DC
\( =>BD = \sqrt {AB.DC} = \sqrt {12,5.28,5} \) \( \approx 18,87 cm\)

Xét \(\Delta ABC\) và \(\Delta BDC\), ta có:
\(\widehat{DAB}=\widehat{DBC}\left(gt\right)\)
\(\widehat{ABD}=\widehat{BDC}\left(AB//CD\right)\)
\(\Rightarrow\Delta ABC\sim\Delta BDC\left(g.g\right)\)
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\Rightarrow BD^2=AB.DC\)
\(\Rightarrow BD=\sqrt{AB.DC}=\sqrt{12,5.28,5}\)
\(\Rightarrow BD\approx18,87cm\) hay \(x\approx18,87cm\)

a, Xét ΔABD và ΔBDC có :
\(\widehat{A}=\widehat{DBC}\left(gt\right)\)
\(\widehat{ABD}=\widehat{BDC}\left(AB//CD;slt\right)\)
\(\Rightarrow\Delta ABD\sim\Delta BDC\left(g-g\right)\)
b, Ta có : \(\Delta ABD\sim\Delta BDC\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{BD}=\dfrac{BD}{DC}\)
hay \(BD^2=AB.DC=12.28,5=342\)
\(\Rightarrow BD=\sqrt{342}\left(cm\right)\)

a: Xét ΔADB và ΔBCD có
\(\widehat{BAD}=\widehat{DBC}\)
\(\widehat{ABD}=\widehat{BDC}\)
Do đó: ΔADB\(\sim\)ΔBCD
b: Ta có: ΔADB\(\sim\)ΔBCD
nên DB/CD=AB/BD=AD/BC
=>5/CD=3/5=3,5/BC
=>CD=25/3(cm); BC=35/6(cm)