Cho tam giác abc có B=50 độ;C=70 độ.Một điểm D thuộc cạnh BC sao cho CAD=40 độ.Tính BAD?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\widehat{C}=180^0-50^0-65^0=65^0=\widehat{B}\)
=>ΔABC cân tại A

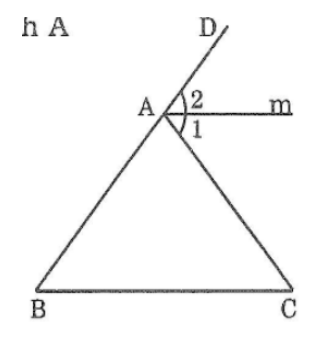
Trong Δ ABC có ∠(CAD ) là góc ngoài đỉnh A
⇒∠(CAD ) =∠B +∠C =50o+50o=100o
(tính chất góc ngoài tam giác)
∠(A1 ) =∠(A2 ) =1/2 ∠(CAD) =50o (vì tia Am là tia phân giác của ∠(CAD)
Suy ra: ∠(A1) =∠C =50o
⇒ Am // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

Từ A kẻ đường cao AH vuông góc với BC , từ B kẻ đường cao BK vuông góc với AC
=> AH = sinC x AC = sin 500 x 35 = a
Ta có : AB = \(\frac{AH}{sinB}=\frac{a}{sinB}=b\)
BK = \(sinA\times AB=sin\left(180^o-60^o-50^o\right)=sin70^o\times b\)= c
=> S . ABC = 1/2AC x BK = 1/2 x 35 x c =..........
a,b,c mình đặt thay cho độ dài AH , AB, BK
Sao bạn không tính hẳn AH, AB, BK mà phải kí hiệu a, b,c vậy?

Kẻ AH vuông góc với BC
Trong tam giác vuông AHC ta có:
\(cosC=\frac{HC}{AC}\Rightarrow HC=cosC.AC=cos50.35\approx22cm\)
\(\Rightarrow AH=\sqrt{AC^2-HC^2}=\sqrt{35^2-22^2}=\sqrt{741}cm\)
Trong tam giác vuông AHB ta có:
\(sinB=\frac{AH}{AB}\Rightarrow AB=\frac{AH}{sinB}=\frac{\sqrt{741}}{sin60}=2\sqrt{247}cm\)
\(\Rightarrow HB=\sqrt{AB^2-AH^2}=\sqrt{\left(2\sqrt{247}\right)^2-741}=\sqrt{247}cm\)
Vậy \(S_{ABC}=\frac{AH\left(HB+HC\right)}{2}=\frac{\sqrt{741}.\left(\sqrt{247}+22\right)}{2}\approx513cm\)

Xét tam giác ABC, có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(80^o+50^o+\widehat{C}=180^o\)
=> \(\widehat{C}=50^o\)
Ta có:
\(\widehat{B}=50^o\)
\(\widehat{C}=50^o\)
Suy ra: \(\widehat{B}=\widehat{C}\)
=> Tam giác ABC cân tại A.
Góc C bằng :
180o-80o-500=50o
vì Góc C =Góc B nên suy ra Tam giác ABC là tam giác cân



Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{A}\) chung
Do đó: ΔABD\(\sim\)ΔACE
Suy ra: AB/AC=AD/AE
hay AB/AD=AC/AE
Xét ΔABC và ΔADE có
AB/AD=AC/AE
\(\widehat{A}\) chung
Do đó: ΔABC\(\sim\)ΔADE
Suy ra: \(\widehat{ABC}=\widehat{ADE}=60^0;\widehat{ACB}=\widehat{AED}=50^0\)
=>\(\widehat{EDC}=120^0;\widehat{DEB}=130^0\)

Bài làm
Xét tam giác ADC có:
\(\widehat{DAC}+\widehat{ACD}=\widehat{ADB}\)( Tổng góc ngoài của tam giác )
hay \(40^0+70^0=\widehat{ADB}\)
\(\Rightarrow\widehat{ADB}=110^0\)
Xét tam giác ADB có:
\(\widehat{ADB}+\widehat{ABD}+\widehat{BAD}=180^0\)(Tổng 3 góc trong tam giác )
hay \(180^0-\left(110^0+50^0\right)=\widehat{BAD}\)
\(\Rightarrow\widehat{BAD}=20^0\)
Vậy \(\widehat{BAD}=20^0\)
# Học tốt #