Cho góc xOy nhọn. Tia phân giác Oz. Trên Ox;Oy lấy A và B;C và D(A nằm giữa O và B;C nằm giữa O và D) sao cho AB =CD. Gọi H và M là trung điểm của AC và BD.Chứng minh: MH song song với Oz
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có hình vẽ:
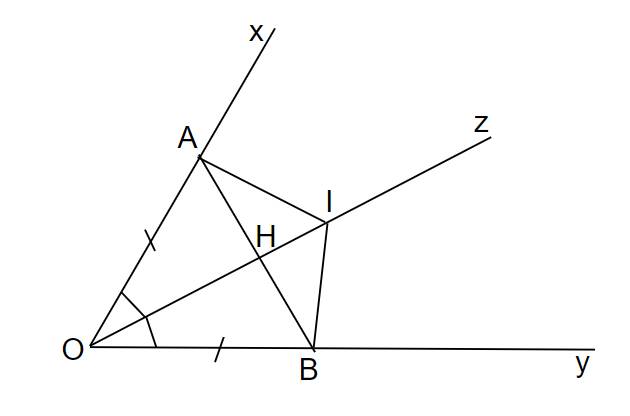
a) Vì Oz là phân giác của xOy nên xOz=yOz=xOy2���=���=���2
Xét Δ AOI và Δ BOI có:
OA = OB (gt)
AOI = BOI (cmt)
OI là cạnh chung
Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)
b) Xét Δ AOH và Δ BOH có:
OA = OB (gt)
AOH = BOH (câu a)
OH là cạnh chung
Do đó, Δ AOH = Δ BOH (c.g.c)
=> AHO = BHO (2 góc tương ứng)
Mà AHO + BHO = 180o (kề bù) nên AHO = BHO = 90o
=> AB⊥OI(đpcm))

a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)'
OC chung
Do đó: ΔOAC=ΔOBC
=>AC=BC và \(\widehat{OAC}=\widehat{OBC}\)
\(\widehat{OAC}+\widehat{xAC}=180^0\)(hai góc kề bù)
\(\widehat{OBC}+\widehat{yBC}=180^0\)(hai góc kề bù)
mà \(\widehat{OAC}=\widehat{OBC}\)
nên \(\widehat{xAC}=\widehat{yBC}\)
b: OA=OB
=>O nằm trên đường trung trực của AB(1)
CA=CB
=>C nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
=>OC\(\perp\)AB
=>Oz\(\perp\)AB

a) ta co :
goc tOy+ goc yOx=90 (2 goc ke phu)
goc zOx+goc yOx=90 ( 2 goc ke phu)
goc yOx= goc yOx ( goc chung )
--> goc tOy= goc zOx
ta co :
goc tOy= goc zOx ( cmt)
goc yOm=goc mOx ( Om la tia p/g gocxOy)
-> goc tOy+goc yOm= goc zOx+ goc mOx==> goc tOm= goc mOz-> Om la tia p/g goc zot
b)ta co
xOy+zOt= 2 xOm+2 mOt =2 (xOm+mOt)=2 xOt =2.90=180