Cho các tập hợp: A=\(\left\{n\in N\backslash n\in BC\left(4;6\right)\right\};B=\left\{n\in N\n\in B\left(12\right)\right\}\\ \)Chứng minh ràng:A=B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
\(A = \left\{ {0;1;2;3;4;5;6} \right\}\)
\(\,B = \left\{ {1;2;3;6;7;8} \right\}\)
Vậy
\(A \cap B = \left\{ {1;2;3;6} \right\}\)
\(A \cup B = \left\{ {0;1;2;3;4;5;6;7;8} \right\} = \left\{ {x \in \mathbb{N}|\;x < 9} \right\}\)
\(A\;{\rm{\backslash }}\;B = \left\{ {0;4;5} \right\}\)
HP
18 tháng 12 2020
a, \(A\cup B=(-4;5]\)
\(A\cap B=[-3;4)\)
\(A\backslash B=\left[4;5\right]\)
\(B\backslash A=\left(-4;-3\right)\)
b, \(A\cup B=\left(-3;7\right)\)
\(A\cap B=[1;2)\cup(3;5]\)
\(A\backslash B=\left[2;3\right]\)
\(B\backslash A=\left(-3;1\right)\cup\left(5;7\right)\)
c, \(A\cup B=\left[\dfrac{1}{2};3\right]\)
\(A\cap B=\left[1;\dfrac{3}{2}\right]\)
\(A\backslash B=[\dfrac{1}{2};1)\)
\(B\backslash A=(\dfrac{3}{2};3]\)
d, \(A\cup B=(-5;2]\cup(3;6]\)
\(A\cap B=\left\{0\right\}\cup[4;5)\)
\(A\backslash B=(0;2]\cup\left[-5;6\right]\)
\(B\backslash A=[-5;0)\cup\left(3;4\right)\)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Ta có: \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\} = \{ - 2; - 1;0;1;2;3\} \)
Và \(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\} = \{ - 2;3\} \)
Khi đó:
Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các phần tử thuộc A mà không thuộc B. Vậy\(A\,{\rm{\backslash }}\,B = \{ - 1;0;1;2\} \).
Tập hợp \(B\,{\rm{\backslash }}\,A\) gồm các phần tử thuộc B mà không thuộc A. Vậy \(B\,{\rm{\backslash }}\,A = \emptyset \)
17 tháng 9 2023
\(A=\left\{x\in R|\left(x-2x^2\right)\left(x^2-3x+2\right)=0\right\}\)
Giải phương trình sau :
\(\left(x-2x^2\right)\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow x\left(1-2x\right)\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\1-2x=0\\x-1=0\\x-2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=1\\x=2\end{matrix}\right.\)
\(\Rightarrow A=\left\{0;\dfrac{1}{2};1;2\right\}\)
\(B=\left\{n\in N|3< n\left(n+1\right)< 31\right\}\)
Giải bất phương trình sau :
\(3< n\left(n+1\right)< 31\)
\(\Leftrightarrow\left\{{}\begin{matrix}n\left(n+1\right)>3\\n\left(n+1\right)< 31\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n^2+n-3>0\\n^2+n-31< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n< \dfrac{-1-\sqrt[]{13}}{2}\cup n>\dfrac{-1+\sqrt[]{13}}{2}\\\dfrac{-1-5\sqrt[]{5}}{2}< n< \dfrac{-1+5\sqrt[]{5}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{-1-5\sqrt[]{5}}{2}< n< \dfrac{-1-\sqrt[]{13}}{2}\\\dfrac{-1+\sqrt[]{13}}{2}< n< \dfrac{-1+5\sqrt[]{5}}{2}\end{matrix}\right.\)
Vậy \(B=\left(\dfrac{-1-5\sqrt[]{5}}{2};\dfrac{-1-\sqrt[]{13}}{2}\right)\cup\left(\dfrac{-1+\sqrt[]{13}}{2};\dfrac{-1+5\sqrt[]{5}}{2}\right)\)
\(\Rightarrow A\cap B=\left\{2\right\}\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
\(E = \{ x \in \mathbb{N}|x < 10\} = \{ 0;1;2;3;4;5;6;7;8;9\} \)
\(A = \{ x \in E|x\) là bội của 3\(\} \)\( = \{ 0;3;6;9\} \)
\(B = \{ x \in E|x\) là ước của 6\(\} \)\( = \{1;2;3;6\} \)
Ta có: \(A\backslash B = \left\{ {0;9} \right\}\), \(B\backslash A = \left\{ {1;2} \right\}\)
\({C_E}A = \{ 1;2;4;5;7;8\} ,\;{C_E}B = \{ 0;4;5;7;8;9\} \)
\(A \cap B = \{ 3;6\} \Rightarrow {C_E}(A \cap B) = {C_E}B = \{0;1;2;4;5;7;8;9\} \)
\(A \cup B = \{ 0;1;2;3;6;9\} \Rightarrow {C_E}(A \cup B) = {C_E}A = \{ 4;5;7;8\} \)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
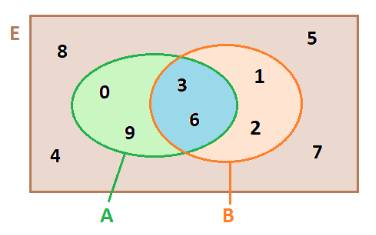
\(E = \{ x \in \mathbb{N}|x < 8\} = \{ 0;1;2;3;4;5;6;7\} \)
a) Ta có: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \)
b) Ta có: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \)
c) Ta có: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)
BCNN(4;6)=12
=>BC(4;6)=B(12)
=>A=B