Khối hộp ABCDA'B'C'D' có đáy là hình chữ nhật với AB=\(\sqrt{3}\) ; AD=\(\sqrt{7}\) . Các đường chéo AC' và DB' lần lượt tao với đáy các góc 45 hoặc 60, chiều cao của nó bằng 2, tính thể tích lăng trụ.
- A.2
- B.4
- C.3
- D.1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là hình chiếu vuông góc của A' trên mặt phẳng (ABCD)
Kẻ HN vuông góc với AB tại N, HM vuông góc với AD tại M
Ta cần tìm chiều cao h=A'H của hình hộp
Dễ dàng chứng minh \(\widehat{A'NH}=60^0\) và \(\widehat{A'MH}=45^0\)
Xét tam giác vuông NHA' và MHB' có
\(NH=\frac{HA'}{tan\widehat{HNA'}}=\frac{h}{\sqrt{3}}\) và \(MH=\frac{HA'}{tan\widehat{HMA'}}=h\)
Xét hình vuông AMHN có \(AH=\sqrt{HN^2+HM^2}=\frac{2h}{\sqrt{3}}\)
Xét tam giác vuông AHA' có \(AH^2+A'H^2=A'A^2\Leftrightarrow h^2+\frac{4}{3}h^2=1\Leftrightarrow h=\sqrt{\frac{3}{7}}\)
Vậy thể tích hình hộp là: \(V=h.\sqrt{3}.\sqrt{7}=\sqrt{\frac{3}{7}}.\sqrt{3}\sqrt{7}=3\)

Chọn A
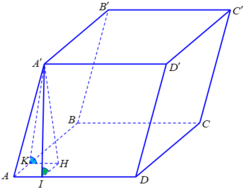
Gọi H là hình chiếu vuông góc của A' lên mặt phẳng (ABCD);

Theo giả thiết, ta có ![]()
=> ΔHKA' = ΔHIA' => HI = HK
=> tứ giác AIHK là hình vuông cạnh a, (a>0) => AH = a√2
Tam giác A'HK vuông cân tại H có HK=HA'=a
Tam giác AHA' vuông tại H có AA'²=AH²+A'H²
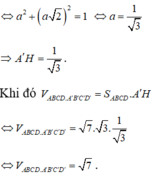

\(AC'=\sqrt{AB^2+AA'^2+AD^2}=\sqrt{11^2+12^2+13^2}=\sqrt{434}\)
S. toàn phần = 2*12*11+2*12*13+2*11*13=862
V hình hộp chữ nhật là 11*12*13=1716
****

Phương pháp:
- Tính thể tích lượng nước trong khối hộp chữ nhật.
- Gọi h là chiều cao mới, lập phương trình ẩn h với chú ý lượng nước trong hộp là không đổi.
Cách giải:
Thể tích nước trước khi đưa khối trụ vào là: V n = 40.50.80 = 160000 c m 3
Gọi h là chiều cao của mực nước sau khi đặt khối trụ vào.
Khi đó thể tích khối hộp chữ nhật chiều cao h là V 1 = 50.80. h = 4000 h
Thể tích khối trụ có chiều cao h là

mình không hiểu rằng bạn muốn tìm thể tích hình lăng trụ nào?có phải là thể tích hình hộp ko?
đầu bài nó chỉ cho như thế thôi, bạn thử tính xem là đáp án nào