Cho tam giác ABC vuông tại A có AB = 12 cm ; AC = 16 cm vẽ AH là đường cao, AM là đường trung tuyến của tam giác ABC
a) Tính BH ; HC ; AH
b) Tính diện tích tam giác HMA .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 9 2021
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
CM
13 tháng 6 2018
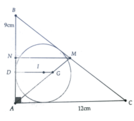
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm
NM
Nguyễn Minh Quang
Giáo viên
19 tháng 2 2022
a. ta có : tam giác AHB vuông tại H nên
\(AH^2=AB^2-BH^2=12^2-7,2^2=9,6^2\) Vậy AH =9,6cm
b. Ta có : ABC phải tam giác vuông vì \(AB^2=BH.BC\)
H9
HT.Phong (9A5)
CTVHS
16 tháng 7 2023
Ta có \(\Delta ABC\) vuông tại A nên:
\(BC^2=AB^2+AC^2\)
Mà: \(AB=\dfrac{2}{3}AC\)
\(\Rightarrow BC^2=\left(\dfrac{2}{3}AC\right)^2+AC^2\)
\(\Rightarrow12^2=\left(\dfrac{2}{3}AC\right)^2+AC\)
\(\Rightarrow144=\dfrac{4}{9}AC^2+AC^2\)
\(\Rightarrow144=\dfrac{13}{9}AC^2\)
\(\Rightarrow AC^2=\dfrac{144}{\dfrac{13}{9}}\approx100\)
\(\Rightarrow AC\approx\sqrt{100}\approx10\left(cm\right)\)
Ta có \(AC=10cm\Rightarrow AB=\dfrac{2}{3}AC=\dfrac{2}{3}\cdot10\approx6,6\left(cm\right)\)
Vậy: ....
16 tháng 6 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
b: BC=căn 9^2+12^2=15cm
AH=9*12/15=7,2cm
15 tháng 3 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=18^2+20^2=724\)
hay \(BC=2\sqrt{181}cm\)
Vậy: \(BC=2\sqrt{181}cm\)
Mấy bài này cũng easy thôi
a) \(\Delta ABC;\widehat{A}=1v\left(gt\right)\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}\)\(=20\left(cm\right)\)
Tam giác ABC đồng dạng với tam giác HBA ( \(\widehat{B}\)chung \(\widehat{BAC}=\widehat{BAH}=90^0\))
\(\Rightarrow\frac{AB}{BH}=\frac{AC}{AH}=\frac{BC}{AB}\)
hay \(\frac{12}{BH}=\frac{16}{AH}=\frac{20}{12}=\frac{10}{6}\)
\(\Rightarrow AH=\frac{16.6}{10}=9,6\left(cm\right)\)
\(\Rightarrow BH=\frac{12.6}{10}=7,2\left(cm\right)\)
\(\Rightarrow HC=BC-BH=20-7,2=12,8\)( cm )
b) \(\Delta HMA\)vuông tại H
\(\Rightarrow S_{HMA}=\frac{1}{2}HM.AH\)\(=\frac{1}{2}.2,8.9,6=13,44\left(cm^2\right)\)