Cho tam giác ABC vuông tại A, đường cao AH
1) Tính độ dài các đoạn thẳng HA, HB và số đo góc C khi biết AB= 3cm; AC= 4cm
2) Đường tròn tâm B bán kính BA cắt đường thẳng AH tại điểm thứ hai là D. Chứng minh rằng bốn điểm A,B,C,D cùng thuộc một đường tròn
3) Vẽ đường kính DE của đường tròn (B). Đường thẳng qua B và vuông góc với DE cắt AD tại I và cắt AE tại F. Gọi K là giao điểm của EI và DF. Chứng minh rằng góc BAK = góc BKA
MN GIẢI GIÚP MK VS! MK ĐANG CẦN GẤP

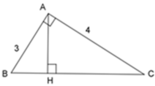
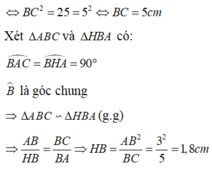


1: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4(cm)
BH=3^2/5=1,8cm
CH=5-1,8=3,2cm
Xet ΔABC vuông tại A có sin C=AB/BC=3/5
nên góc C=37 độ
2: ΔBAD cân tại B
mà BH là đường cao
nên BH là phân giác của góc ABD
Xet ΔABC và ΔDBC co
BA=BD
góc ABC=góc DBC
BC chung
Do đó: ΔABC=ΔDBC
=>góc BDC=90 độ
=>CD là tiếp tuyến của (B)
Cậu tự vẽ hình nhé
a) Xét △ABC vuông tại A, có đường cao AH
BC2=AB2 + AC2 (pytago)
BC2= 32 + 42
BC2 = \(\sqrt{9+16}\)
BC =5
Xét △ABC vuông tại A
AC2= BC x BH
42=5 x BH
BH= 16 : 5
BH = 3,2
Xét △ ABC vuông tại A
AB x AC = BC x AH
3 x 4 = 5 x AH
AH =12 :5
AH= 2,4Xét △ABC vuông tại A ta có:Sin C = \(\dfrac{AB}{BC}\)
Sin C = \(\dfrac{3}{5}\)
➩ góc C = 37o
b) △BAD cân tại B
➩BH là đường cao
➩BH là phân giác của \(\widehat{ABD}\)
Xét △ ABC và △ BDC ta có:
➜ BA= BD
\(\widehat{ABC}\) =\(\widehat{BDC}\)
BC chung
➩△ABC = △BDC
➩ CD là t/t của B