Cho ΔABC có AB=5cm; AC=12cm. Tính bán kính đường tròn ngoại tiếp của tam giác đó.
Giúp e vs nak....^^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 2 2023
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
19 tháng 8 2021
Kẻ BH vuông góc với AC tại H.
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta được:
\(BH=sinA\cdot AB=sin60^0.4=2\sqrt{3}\left(cm\right)\)
\(AH=cosA.AB=cos60^0.4=2\left(cm\right)\)
Suy ra BH = 3(cm).
Áp dụng định lý Py-ta-go vào tam giác BHC vuông tại H, ta được:
\(BC=\sqrt{BH^2+CH^2}=\sqrt{12+9}=\sqrt{21}\left(cm\right)\)
Vậy BC = \(\sqrt{21}\)(cm)
8 tháng 4 2022
ta có : ΔABC~ΔDEF (gt)
=>\(\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{\text{EF}}=k\)
=> DE = 3:2= 1,5 (cm)
DF = 4:2 = 2 (cm)
BC = 5:2 = 2,5 (cm )
=> Chu vi tam giác DEF = DE+DF+BC = 1,5+2+2,5 = 6(CM)
8 tháng 4 2022
Ta có:
\(\dfrac{AB}{DE}=2;\dfrac{AC}{DF}=2;\dfrac{BC}{EF}=2\)
\(\Leftrightarrow\dfrac{3}{DE}=2;\dfrac{4}{DF}=2;\dfrac{5}{EF}=2\)
\(\Leftrightarrow DE=\dfrac{3}{2};DF=\dfrac{4}{2};EF=\dfrac{5}{2}\)
\(\Rightarrow C_{DEF}=\dfrac{3}{2}+\dfrac{4}{2}+\dfrac{5}{2}=\dfrac{12}{2}=6\left(cm\right)\)
28 tháng 6 2023
a: BC^2=AB^2+AC^2
=>ΔABC vuông tại A
b: góc BAD+góc EAD=90 độ
góc BDA+góc HAD=90 độ
mà góc BAD=góc BDA
nên góc EAD=góc HAD
=>AD là phân giác của góc HAC
c: Xét ΔAHD và ΔAED có
AH=AE
góc HAD=góc EAD
AD chung
=>ΔAHD=ΔAED
=>góc AED=góc AHD=90 độ
=>DE vuông góc AC
27 tháng 2 2022
Xét tam giác vuông ABC có:
\(AB^2+AC^2=BC^2\\ =>3^2+AC^2=5^2\\ =>AC^2=16\\ =>AC=4cm\)
9 tháng 6 2021
a, \(\Delta ABC\sim\Delta CBD\)
\(\dfrac{AB}{CB}=\dfrac{BC}{BD}=\dfrac{4}{6}=\dfrac{6}{4+5}=\dfrac{2}{3}\)
b, \(\dfrac{AC}{CD}=\dfrac{AB}{CB}=\dfrac{2}{3}\)
\(\Rightarrow CD=\dfrac{3AC}{2}=\dfrac{15}{2}\)
-Chúc bạn học tốt-
DH
1
H9
HT.Phong (9A5)
CTVHS
19 tháng 8 2023
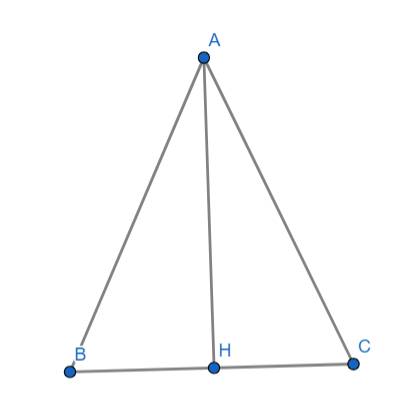
Do tam giác ABC là tam giác cân nên AH là đường cao đồng thời là đường trung tuyến nên:
\(BH=CH=\dfrac{BC}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
Xét tam giác vuông ABH ta có:
\(sinB=\dfrac{BH}{AB}\)
\(\Rightarrow sin40^{o0}=\dfrac{2,5}{AB}\Rightarrow AB=\dfrac{2,5}{sin40^o}\approx4\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác đó ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{4^2-2,5^2}\approx3\left(cm\right)\)
2 tháng 10 2021
Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)