Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét tam giác vuông OAB:
\(OB=\sqrt{AB^2-OA^2}=4\)
Áp dụng hệ thức lượng cho tam giác vuông ABD với đường cao AO:
\(AB^2=OB.BD\Rightarrow BD=\dfrac{AB^2}{OB}=13\)
\(\Rightarrow\left\{{}\begin{matrix}OD=BD-OB=9\\AD=\sqrt{BD^2-AB^2}=\sqrt{29}\end{matrix}\right.\)
\(\widehat{BAO}=\widehat{DCO}\left(slt\right)\Rightarrow\Delta_VAOB\sim\Delta_VCOD\) (g.g)
\(\Rightarrow\dfrac{AB}{DC}=\dfrac{OB}{OD}\Rightarrow DC=\dfrac{AB.OD}{OB}=\dfrac{9\sqrt{13}}{2}\)
\(S_{ABCD}=\dfrac{1}{2}AD.\left(AB+CD\right)=\dfrac{1}{2}.\sqrt{29}.\left(2\sqrt{13}+\dfrac{9\sqrt{13}}{2}\right)=...\)
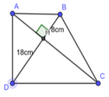
Xét ∆ ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
⇒ A H 2 = HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ∆ ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
⇒ H D 2 = H A . H C ⇒ 18 2 = 12 H C => HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
S A B C D = A C . B D 2 = 26.39 2 = 507 c m 2
Đáp án cần chọn là: D
a: Kẻ CK\(\perp\)AB; AH\(\perp\)DC
=>CK,AH là các đường cao của hình thang ABCD
=>CK=AH
\(S_{ADC}=\dfrac{1}{2}\times AH\times DC\)
\(S_{ABC}=\dfrac{1}{2}\times CK\times AB\)
mà CK=AH
nên \(\dfrac{S_{ADC}}{S_{ABC}}=\dfrac{CD}{AB}=3\)
=>\(S_{ADC}>S_{ABC}\)
b: AB//CD
nên \(\dfrac{MA}{MD}=\dfrac{AB}{CD}=\dfrac{1}{3}\)
=>\(\dfrac{S_{MAB}}{S_{MDC}}=\left(\dfrac{MA}{MD}\right)^2=\dfrac{1}{9}\)
=>\(S_{MDC}=9\times S_{MAB}\)
\(S_{MAB}+S_{ABCD}=S_{MDC}\)
=>\(S_{ABCD}=9\times S_{MAB}-S_{MAB}=8\times S_{MAB}\)
=>\(S_{AMB}=\dfrac{60}{8}=7,5\left(cm^2\right)\)