Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

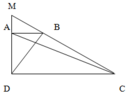
a. S A B C = 1 3 S A D C (Vì cùng chung chiều cao của hình thang ABCD; đáy AB = 1 3 DC)
b. S A B M = S A C M (Vì cùng chung đáy MA, chiều cao AB = 1 3 DC )
c. Theo phần a, ta có: S A B C = S A D C
Mà S A B C D = S A B C + S A D C
Nên S A B C = 1 1 + 3 S A B C D = 1 4 S A B C D
Do đó S A B C D = 64 × 1 4 = 16 ( c m 2 )
Theo phần b, ta có: S A B M = 1 3 S A C M
Mà S A C M = S M A B + S A B C
Nên S M A B = 1 3 - 1 S A B C = 1 2 S A B C
Do đó S M A B = 16 × 1 4 = 8 ( c m 2 )

Xin loi bai nay minh ko ve duoc hinh.Thong cam cho minh nhe !!!
a)S_ABC = 1/3 S_ADC (Đáy AB = 1/3 đáy CD; Chiều cao hạ xuống đáy từ C bằng chiều cao hạ từ A)
b)S_ABM = 1/3 S_CAM (Đáy AM chung; chiều cao hạ từ B bằng 1/3 chiều cao hạ từ B xuống đáy AM)
c)
S_ABC = 1/3 S_ACD (câu trên) => S_ABC = 1/4 S_ABCD = 64 : 4 = 16 cm2
Mà: S_ABM = 1/3 S_ACM (câu trên) => S_ABM = 1/2 S_ABC = 16 : 2 = 8 cm2

Bài giải
a) Do đề bài không cập nhật độ dài của hình thang ABCD nên ta gọi chiều cao là AD ( với AD = BC ), độ dài cạnh DC là 13 ×3=1cm. Vậy, diện tích hình tam giác ABC là :
13 ×AD2 =16 AD( cm2 )
Diện tích hình tam giác ADC là :
\(\frac{1\times AD}{2}=\frac{1}{2}AD\left(cm^2\right)\)
Vì : \(\frac{1}{6}AD< \frac{1}{2}AD\)
nên diện tích hình tam giác ADC lớn hơn diện tích hình tam giác ABC.

Bài giải
a) Do đề bài không cập nhật độ dài của hình thang ABCD nên ta gọi chiều cao là AD ( với AD = BC ), độ dài cạnh DC là \(\frac{1}{3}\times3=1\)cm. Vậy, diện tích hình tam giác ABC là :
\(\frac{\frac{1}{3}\times AD}{2}=\frac{1}{6}AD\)( cm2 )
Diện tích hình tam giác ADC là :
\(\frac{1\times AD}{2}=\frac{1}{2}AD\)( cm2 )
Vì \(\frac{1}{6}AD<\frac{1}{2}AD\)nên diện tích hình tam giác ADC lớn hơn diện tích hình tam giác ABC.
bạn kia lm sai rồi!
lấy 1/3 x với ac=abc
lấy 3/3 x vơi ac[với ac =ad]=adc
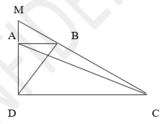

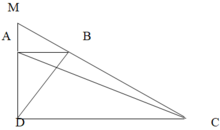
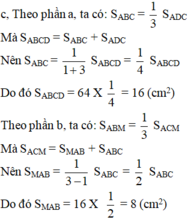
a: Kẻ CK\(\perp\)AB; AH\(\perp\)DC
=>CK,AH là các đường cao của hình thang ABCD
=>CK=AH
\(S_{ADC}=\dfrac{1}{2}\times AH\times DC\)
\(S_{ABC}=\dfrac{1}{2}\times CK\times AB\)
mà CK=AH
nên \(\dfrac{S_{ADC}}{S_{ABC}}=\dfrac{CD}{AB}=3\)
=>\(S_{ADC}>S_{ABC}\)
b: AB//CD
nên \(\dfrac{MA}{MD}=\dfrac{AB}{CD}=\dfrac{1}{3}\)
=>\(\dfrac{S_{MAB}}{S_{MDC}}=\left(\dfrac{MA}{MD}\right)^2=\dfrac{1}{9}\)
=>\(S_{MDC}=9\times S_{MAB}\)
\(S_{MAB}+S_{ABCD}=S_{MDC}\)
=>\(S_{ABCD}=9\times S_{MAB}-S_{MAB}=8\times S_{MAB}\)
=>\(S_{AMB}=\dfrac{60}{8}=7,5\left(cm^2\right)\)