Câu 1 : gọi(d) là đt y=(2k-1)x+k-2 với k tham số
a, tìm k để (d) đi qua điểm (1;6)
b,tìm k để (d) song song với đt 2x+3y-5=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 11 2015
a, b=k=0
b,(2k-1).3+k=0 => 3k=3 => k =1
c, 2k-1 = 3/5=> 2k = 8/5 => k = 4/5 khác 4 vậy k = 4/5
d, (2k-1)(-3) +k =2 => -5k =-1 => k =1/5
13 tháng 12 2023
a: Tọa độ A là;
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=0\end{matrix}\right.\)
Vậy: A(3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-x+3=-0+3=3\end{matrix}\right.\)
Vậy: B(0;3)
O(0;0); A(3;0); B(0;3)
\(OA=\sqrt{\left(3-0\right)^2+\left(0-0\right)^2}=3\)
\(OB=\sqrt{\left(0-0\right)^2+\left(3-0\right)^2}=\sqrt{0^2+3^2}=3\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{9}{2}\)
b:
Để (d1) cắt (d2) thì k+1<>-1
=>k<>-2
Phương trình hoành độ giao điểm là:
(k+1)x+1=-x+3
=>(k+1)x+x=2
=>x(k+2)=2
=>\(x=\dfrac{2}{k+2}\)
Để hoành độ là số nguyên nhỏ nhất thì \(\dfrac{2}{k+2}\) là số nguyên nhỏ nhất có thể
=>k+2=-1
=>k=-3
PC
13 tháng 5 2018
Lời giải:
Gọi đường thẳng (d)(d) có dạng y=kx+by=kx+b. Vì I(0;1)∈(d)⇒b=1⇒(d):y=kx+1I(0;1)∈(d)⇒b=1⇒(d):y=kx+1
Phương trình hoành độ giao điểm x2+kx+1=0x2+kx+1=0.
Theo đó, nếu A,B=(d)∩(P)A,B=(d)∩(P) thì áp dụng hệ thức Viet ta có: x1+x2=−kx1+x2=−k
Trung điểm của ABAB là II nằm trên trục trung khi 0=xI=x1+x22=−k2⇒k=00=xI=x1+x22=−k2⇒k=0
Do đó k=0k=0 là kết quả cần tìm.
AH
Akai Haruma
Giáo viên
4 tháng 1
Lời giải:
** Sửa lại hàm số: $y=-x+3$
a. Bạn có thể tự vẽ.
b. Để $y=(2k-1)x+1$ song song với (d)$ thì:
$2k-1=-1$
$\Leftrightarrow k=0$
c. PT hoành độ giao điểm của $(d)$ và $y=(k-3)x+5$:
$-x+3=(k-3)x+5$
$\Leftrightarrow (k-2)x=-2$
$\Leftrightarrow x=\frac{-2}{k-2}$ (đk: $k\neq 2$)
Khi đó: $y=-x+3=\frac{2}{k-2}+3$
Hai đths cắt nhau tại điểm có tung độ $7$
$\Leftrightarrow \frac{2}{k-2}+3=7$
$\Leftrightarrow \frac{2}{k-2}=4$
$\Leftrightarrow k-2=\frac{1}{2}\Leftrightarrow k=2,5$
4 tháng 1
a: Sửa đề: y=-x+3
Vẽ đồ thị
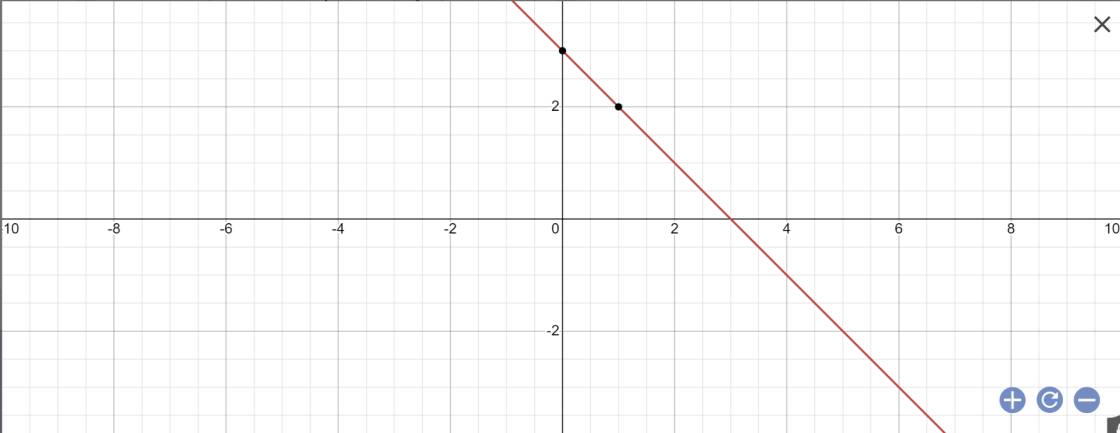
b: Để đường thẳng y=(2k-1)x+1 song song với (d) thì
\(\left\{{}\begin{matrix}2k-1=-1\\1\ne3\left(đúng\right)\end{matrix}\right.\)
=>2k-1=-1
=>2k=0
=>k=0
c: Thay y=7 vào y=-x+3, ta được:
-x+3=7
=>-x=4
=>x=-2
Thay x=-2 và y=7 vào y=(k-3)x+5, ta được:
-2(k-3)+5=7
=>-2(k-3)=2
=>k-3=-1
=>k=2
a/ Vì \(\left(1;6\right)\in\left(d\right)\)
Thay x=1; y=6 vào (d) có:
2k-1+k-2=6
\(\Leftrightarrow k=3\)
b/ \(y=\frac{5-2x}{3}=\frac{-2}{3}x+\frac{5}{3}\)
Để (d)// đt \(y=\frac{-2}{3}x+\frac{5}{3}\Leftrightarrow\left\{{}\begin{matrix}2k-1=\frac{-2}{3}\\k-2\ne\frac{5}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}k=\frac{1}{6}\\k\ne\frac{11}{3}\end{matrix}\right.\Leftrightarrow k=\frac{1}{6}\)