Giúp tôi câu này
Cho M (1;3).Tìm hàm số y=ax+b. biết đồ thị của nó đi qua điểm M cắt 2 trục Ox và Oy tại A và B
Tìm hàm số y=ax+b sao cho S ΔOAB min
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\Rightarrow2a=1\Rightarrow a=\dfrac{1}{2}\Rightarrow y=\dfrac{1}{2}x\\ c,\text{Thay }x=6;y=3\Rightarrow3=\dfrac{1}{2}\cdot6\left(đúng\right)\\ \Rightarrow N\left(6;3\right)\in y=ax\)

a. \(M\left(2;1\right)\Rightarrow1=2a\Rightarrow a=\dfrac{1}{2}\)

Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow xy+yz+zx=1\)
\(P=\sqrt{\dfrac{yz}{x^2+1}}+\sqrt{\dfrac{zx}{y^2+1}}+\sqrt{\dfrac{xy}{z^2+1}}\)
\(P=\sqrt{\dfrac{yz}{x^2+xy+yz+zx}}+\sqrt{\dfrac{zx}{y^2+xy+yz+zx}}+\sqrt{\dfrac{xy}{z^2+xy+yz+zx}}\)
\(P=\sqrt{\dfrac{yz}{\left(x+y\right)\left(x+z\right)}}+\sqrt{\dfrac{zx}{\left(y+z\right)\left(x+y\right)}}+\sqrt{\dfrac{xy}{\left(x+z\right)\left(y+z\right)}}\)
\(P\le\dfrac{1}{2}\left(\dfrac{y}{x+y}+\dfrac{z}{x+z}\right)+\dfrac{1}{2}\left(\dfrac{z}{y+z}+\dfrac{x}{x+y}\right)+\dfrac{1}{2}\left(\dfrac{x}{x+z}+\dfrac{y}{y+z}\right)=\dfrac{3}{2}\)
\(P_{max}=\dfrac{3}{2}\) khi \(x=y=z=\dfrac{1}{\sqrt{3}}\) hay \(a=b=c=\sqrt{3}\)

xét ΔADM và ΔADN có:
AD chung
MAD=NAD(góc)
AMD=AND=90(góc)
⇒ΔADM=ΔADN(cạnh huyền--góc nhọn)

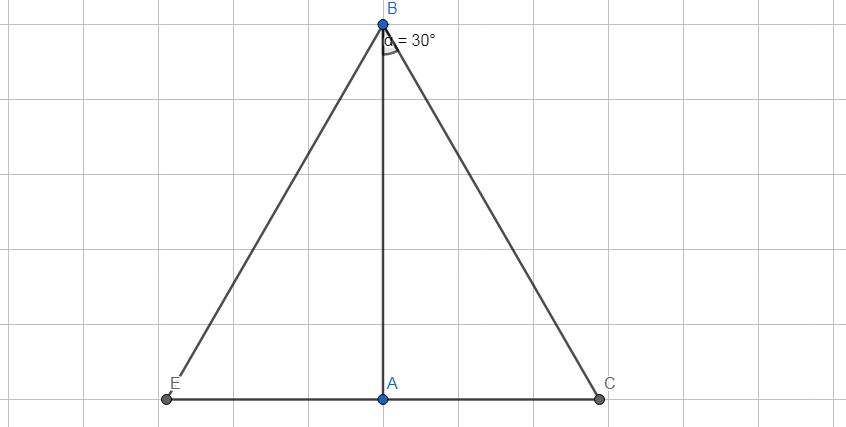
a) Xét tam giác ABC vuông tại A có:
\(\widehat{ABC}+\widehat{ACB}=90^0\)(phụ nhau)
=>300+\(\widehat{ACB}\)=900
=>\(\widehat{ACB}\)=600
Xét tam giác BEC có:
BA là đường cao (BA vuông góc với EC tại A)
BA là trung tuyến (A là trung điểm EC)
=>Tam giác BEC cân tại B mà \(\stackrel\frown{BCE}=60^0\)(cmt)
=>Tam giác BEC đều.
i dell bt