Trong mặt phẳng Oxy, cho M(;1) và N(√3;3). Khẳng định nào sau đây là đúng?
A. M O N ^ = 60 0 .
B. M O N ^ = 30 0 .
C. M O N ^ = 120 0 .
D. M O N ^ = 150 0 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

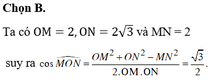

a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)

Cho điểm M(x;y) bất kì, xác định \({M_1},{M_2}\) lần lượt là hình chiếu vuông góc của M xuống trục hoành và trục tung
Dễ thấy \(\overrightarrow {O{M_1}}= x\overrightarrow i ; \, \overrightarrow {O{M_2}} = y \overrightarrow j \)
Áp dụng quy tắc hình bình hành ta có \(\overrightarrow {OM} = \overrightarrow {O{M_1}} + \overrightarrow {O{M_2}} = x\overrightarrow i + y\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow {OM} \) là (x;y), trùng với tọa độ điểm M.

![]()
Suy ra mặt phẳng (ABC) có một VTPT là ![]()
Mặt phẳng (Oxy) có một VTPT là k → = 0 ; 0 ; 1
Gọi φ là góc giữa hai mặt phẳng (ABC) và (Oxy). Ta có
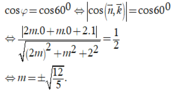
Chọn C.