Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;3) và mặt phẳng P : x + m y + ( 2 m + 1 ) z - ( 2 + m ) = 0 với m là tham số. Gọi điểm H(a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn nhất.
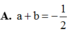
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Gọi I là trung điểm của 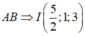
Ta có: ![]()
![]()
IA²+IB² không đổi nên MA²+MB² đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=> M là hình chiếu của I trên trục Oz.
=> M (0;0;3).

Chọn C
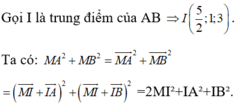
IA²+IB² không đổi nên MA²+MB² đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
Suy ra M là hình chiếu của I trên trục Oz.
Suy ra M (0;0;3).

Chọn C
Gọi I là trung điểm của AB 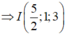
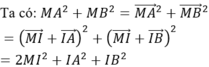
Suy ra: MA2 + MB2 đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=>M là hình chiếu của I trên trục Oz => M (0 ; 0 ; 3)

Đáp án C.
Ta có phương trình mặt phẳng (P) đi qua M và vuông góc với d
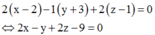
Gọi I là giao điểm của đường thẳng d và (P) khi đó tạo độ I là nghiệm của hệ
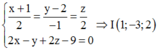
M’ đối xứng với M qua d thì I là trung điểm của MM’ ⇒ M’(0;-3;3)
Đáp án D.