Chứng minh: BCNN(20;25) = 20.25 chia ƯCLN(20;25)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Ta có:8=23
10=2.5
24=24.5
BCNN(...)=23.5=24.5=40
b)Ta có:
16=24
24=23.3
BCNN(...)=24.3=48
c)Ta có:
60=22.3.5
140=22.5.7
BCNN(...)=22.3.5.7=420
Mấy bài sau bn cứ lm như thế này nhé^^

a) 8 = 2³
10 = 2.5
20 = 2².5
BCNN(8; 10; 20) = 2³.5 = 40
b) 16 = 2⁴
24 = 2³.3
BCNN(16; 24) = 2⁴.3 = 48
c) 60 = 2².3.5
140 = 2².5.7
BCNN(60; 140) = 2².3.5.7 = 420
d) 8 = 2³
9 = 3²
11 = 11
BCNN(8; 9; 11) = 2³.3².11 = 792
e) 24 = 2³.3
40 = 2³.5
162 = 2.3⁴
BCNN(24; 40; 162) = 2³.3⁴.5 = 3240
f) 56 = 2³.7
70 = 2.5.7
126 = 2.3².7
BCNN(56; 70; 126) = 2³.3².5.7 = 2520
g) 28 = 2².7
20 = 2².5
30 = 2.3.5
BCNN(28; 20; 30) = 2².3.5.7 = 420
h) 34 = 2.17
32 = 2⁵
20 = 2².5
BCNN(34; 32; 20) = 2⁵.5.17 = 2720
k) 42 = 2.3.7
70 = 2.5.7
20 = 2².5
BCNN(42; 70; 20) = 2².3.5.7 = 420
l) 9 = 3²
10 = 2.5
11 = 11
BCNN(9; 10; 11) = 2.3².5.11 = 990

Gọi \(d=ƯC\left(n;n+1\right)\)
\(\Rightarrow\left(n+1\right)-n⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
\(\Rightarrow n\) và \(n+1\) nguyên tố cùng nhau
\(\Rightarrow BCNN\) của n và n+1 là \(n\left(n+1\right)=n^2+n\) (đpcm)

\(Goi:d=UCLN\left(a;b\right)\Rightarrow a=da';b=db'\left(UCLN\left(a';b'\right)=1\right)\)
\(\Rightarrow BCNN\left(a,b\right)=a'b'd\Rightarrow UCLN\left(a,b\right).BCNN\left(a,b\right)=a'b'd^2=ab=a'b'd^2\)
Đặt d = ƯCLN( a,b)=> a = d.a'
( a',b') =1
b=d.b'
Ta cần chứng minh : BCNN( a,b).d=a.b hay BCNN ( a,b)=\(\frac{a.b}{d}\)
Đặt m = \(\frac{a.b}{d}\)
m = b . \(\frac{a}{d}\)=b. a'
Mà ( a',b') =1 => m \(\in\)BCNN (a,b)=> BCNN( a,b )=\(\frac{a.b}{d}\)
BCNN(a,b )=\(\frac{a.b}{ƯCLN\left(a,b\right)}\)
=> BCNN( a,b ) . ƯCLN( a,b ) =a.b
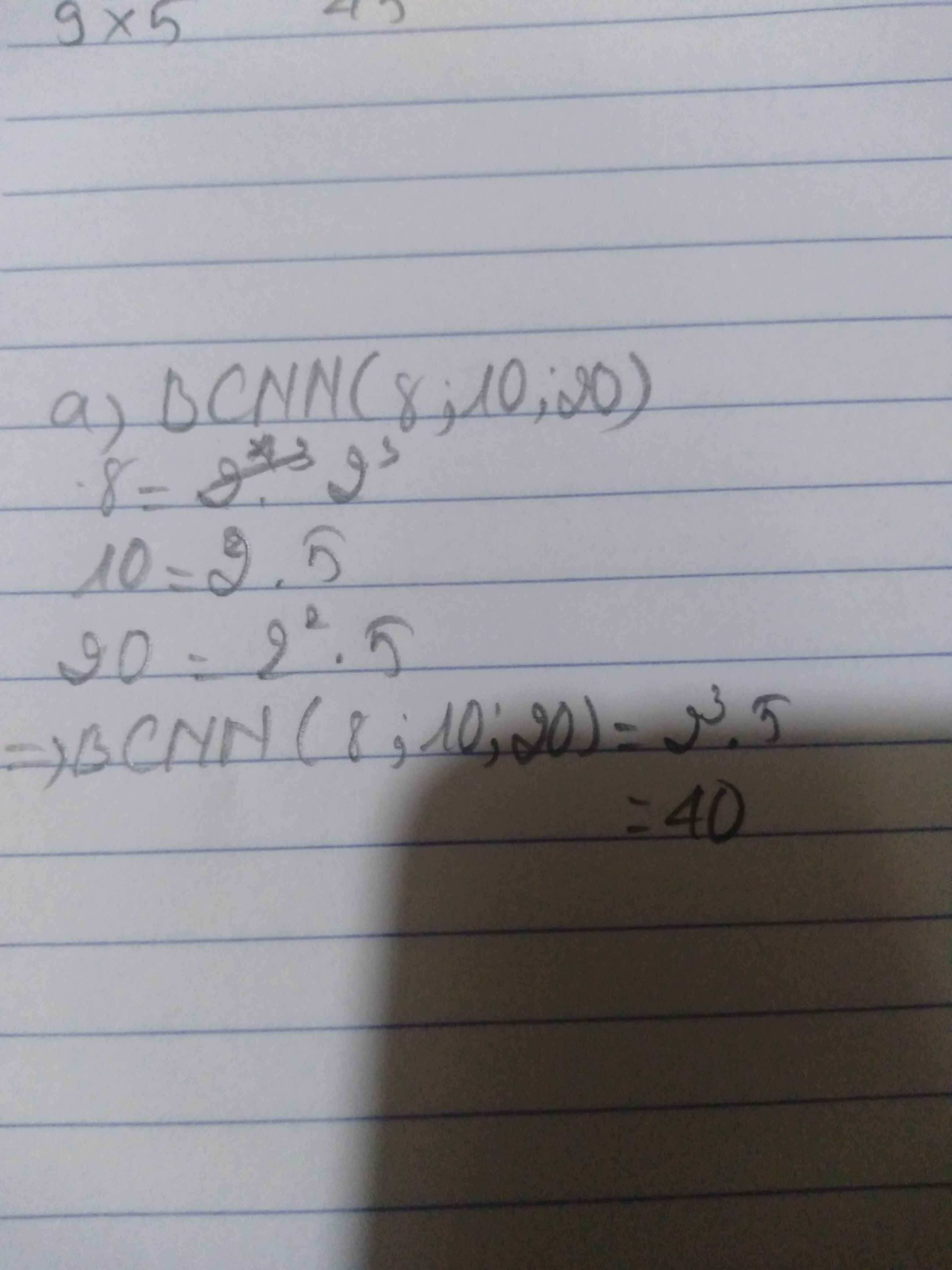
BCNN(20;25)
20=2\(^2\).5
25=5\(^2\)
vậy BCNN(20;25)=2\(^2\). 5\(^2\)=100