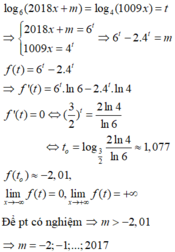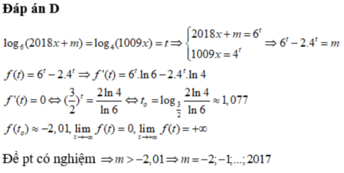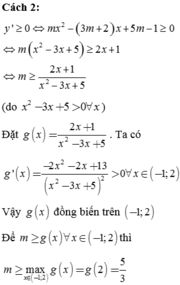Số các giá trị nguyên của tham số m ∈ [-2018; 2018] để PT: \(x^2+\left(2-m\right)x+4=4\sqrt{x^3+4x}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 2 2017
Đáp án B
Ta có y ' = m x 2 − 3 m + 2 x + 5 m − 1
Để hàm số đồng biến trên khoảng − 1 ; 2 thì y ' ≥ 0, ∀ x ∈ − 1 ; 2 .Dấu bằng xảy ra tại hữu hạn điểm
Cách 1:
Do ta chỉ xét giá trị m nguyên âm nên m x 2 − 3 m + 2 x + 5 m − 1 = 0 là phương trình bậc hai. Đặt f x = m x 2 − 3 m + 2 x + 5 m − 1
TH1: Hàm số có hai điểm cực trị
Để thỏa mãn y ' ≥ 0, ∀ x ∈ 0 ; 2 thì phương trình y ' = 0 có hai nghiệm x 1 ; x 2 thỏa mãn x 1 ≤ − 1 < 2 ≤ x 2
⇔ m . f − 1 ≤ 0 m . f 2 ≤ 0 ⇔ m . m + 3 m + 2 + 5 m − 1 ≤ 0 m . 4 m − 2 3 m + 2 + 5 m − 1 ≤ 0
⇔ m 9 m + 1 ≤ 0 m 3 m − 5 ≤ 0 ⇔ m ≥ − 1 9 m ≥ 5 3 ⇔ m ≥ 5 3
(do m nguyên âm nên không thỏa mãn)
TH2: Hàm số không có điểm cực trị
Để thỏa mãn yêu cầu đề bài thi Δ < 0 m > 0 (do m nguyên âm nên không thỏa mãn)
Vậy ta chọn B.
Cách 2:
y ' ≥ 0 ⇔ m x 2 − 3 m + 2 x + 5 m − 1 ≥ 0 ⇔ m x 2 − 3 x + 5 ≥ 2 x + 1 ⇔ m ≥ 2 x + 1 x 2 − 3 x + 5
(do x 2 − 3 x + 5 > 0 ∀ x )
Đặt g x = 2 x + 1 x 2 − 3 x + 5 . Ta có g ' x = − 2 x 2 − 2 x + 13 x 2 − 3 x + 5 2 > 0 ∀ x ∈ − 1 ; 2 . Vậy g x đồng biến trên − 1 ; 2
Để m ≥ g x ∀ x ∈ − 1 ; 2 thì m ≥ max x ∈ − 1 ; 2 g x = g 2 = 5 3
CM
30 tháng 9 2019
Hàm số bậc nhất đồng biến suy ra a > 0 hay m > 2
m thuộc đoạn [-2018; 2018] suy ra m thuộc {3; 4; ...; 2018}
Vậy có 2016 giá trị nguyên của m cần tìm.
Chọn D.
CM
9 tháng 5 2018
Đáp án A
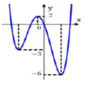
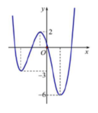
Đồ thị hàm số y = f x có 3 điểm cực trị Đồ thị hàm số y = f x + 2018 có 3 điểm cực trị
Dựa vào ĐTHS y = f x ⇒ y = f x + 2018 có 7 điểm cực trị
Do đó, để hàm số y = f x + 2018 + 1 3 m 2 có 5 điểm cực trị khi và chỉ khi 3 ≤ 1 3 m 2 ≤ 6
Kết hợp với điều kiện m ∈ ℤ + suy ra m = 3 ; 4
Chú ý: Đồ thị hàm số y = f x + C được cho bởi cách tịnh tiến đồ thị hàm số theo trục Oy C đơn vị