Có tất cả bao nhiêu giá trị nguyên của tham số m \(\in\) (-20;20) để 3.log2(\(\frac{8x-2^{x^{ }}-12m}{3}\)) - \(2^x\) - \(x\) = 3m có đúng hai nghiệm thực phân biệt ?
A. 19 B. 18 C. 20 D. 21
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
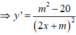
Để hàm số nghịch biến trên khoảng (0;2) thì
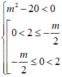
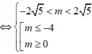
![]()
Mà m ∈ ℤ
⇒ m ∈ - 4 ; 0 ; 1 ; 2 ; 3 ; 4 : có 6 giá trị
Chọn: B

![]()
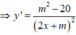
Để hàm số nghịch biến trên khoảng (0;2) thì
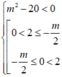
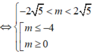
![]()
Mà m ∈ ℤ
⇒ m ∈ - 4 ; 0 ; 1 ; 2 ; 3 ; 4 : có 6 giá trị
Chọn: B

b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)

Đáp án D
Nhắc lại quy tắc vẽ đồ thị hàm số y = f x từ đồ thị hàm số y = f x
- Phần 1: Giữ nguyên phần đồ thị hàm số y = f x bên phải trục Oy (bỏ phần bên trái)
- Phần 2: Lấy đối xứng phần đồ thị hàm số y = f x bên phải trục O qua trục O
- Hợp của 2 phần, ta được đồ thị hàm số y = f x
Xét y = f x = 1 3 x 3 − 2 x 2 + m − 1 x + 3 với f x = 1 3 x 3 − 2 x 2 + m − 1 x + 3
Để hàm số y = f x có 5 điểm cực trị ⇔ y = f x có 2 điểm cực trị nằm phía bên phải trục Oy ⇔ f ' x = 0 có 2 nghiệm dương phân biệt ⇔ x 2 − 4 x + m − 1 = 0 có 2 nghiệm dương phân biệt x 1 , x 2
⇔ Δ > 0 x 1 + x 2 > 0 x 1 x 2 > 0 ⇔ 5 − m > 0 m − 1 > 0 ⇔ 1 < m < 5 . Kết hợp m ∈ ℤ → m = 2 ; 3 ; 4

⇔ x − 1 ≥ 0 2 x + m = x − 1 2 ⇔ x ≥ 1 x 2 − 4 x + 1 − m = 0 ( * )
Phương trình có nghiệm duy nhất khi hệ có nghiệm duy nhất.
![]()
TH1: ∆ ' = 0 ⇔ m = - 3 thì (*) có nghiệm kép x = 2 ≥ 1 (thỏa).
TH2: ∆ ' > 0 ⇔ m > - 3 thì phương trình có nghiệm duy nhất khi (*) có 2 nghiệm thỏa mãn:
x 1 < 1 < x 2 ⇔ x 1 - 1 x 2 - 1 < 0 ⇔ x 1 x 2 - x 1 + x 2 + < 0
⇔ 1 - m - 4 + < 0 ⇔ m > - 2
Do m không dương nên m ∈ {−1; 0}
Kết hợp với trường hợp m = −3 ở trên ta được 3 giá trị của m thỏa mãn bài toán.
Đáp án cần chọn là: B

Đáp án D
Ta có y ' = 3 m + 1 x 2 + 2 m + 1 x − 2
Để hàm số y = m + 1 x 3 + m + 1 x 2 − 2 x + 2 nghịch biến trên ℝ thì y ' ≤ 0 với ∀ x ∈ ℝ
Suy ra 3 m + 1 x 2 + 2 m + 1 x − 2 ≤ 0 với ∀ x ∈ ℝ , ⇒ a = 0 b x + c ≤ 0 a ≠ 0 a < 0 Δ ' ≤ 0
m = − 1 − 2 ≤ 0 l / d m < − 1 m 2 + 8 m + 7 ≤ 0 ⇔ m = − 1 m ∈ − 7 ; − 1 . Theo đầu bài: m ∈ ℤ ⇒ m = − 7 ; − 6 ; − 5 ; − 4 ; − 3 ; − 2 ; − 1
Đặt \(log_2\left(\frac{8x-2^x-12m}{3}\right)=t\)
\(\Rightarrow8x-2^x-12m=3.2^t\)
Ta được hệ: \(\left\{{}\begin{matrix}3t-2^x-x=3m\\8x-2^x-3.2^t=12m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}12t-4.2^x-4x=12m\\8x-2^x-3.2^t=12m\end{matrix}\right.\)
\(\Rightarrow12t-3.2^x-12x+3.2^t=0\)
\(\Leftrightarrow3.2^t+12t=3.2^x+12x\)
Hàm \(f\left(a\right)=3.2^a+12a\) đồng biến trên R nên đẳng thức xảy ra khi và chỉ khi \(x=t\)
\(\Rightarrow3x-2^x-x=3m\)
\(\Leftrightarrow2x-2^x=3m\)
Khảo sát hàm \(f\left(x\right)=2x-2^x\Rightarrow f'\left(x\right)=2-2^x.ln2=0\)
\(\Rightarrow2^x=\frac{2}{ln2}\Rightarrow x=log_2\left(\frac{2}{ln2}\right)=1-log_2\left(ln2\right)\)
Từ BBT ta thấy để pt có đúng 2 nghiệm thực pb
\(\Leftrightarrow3m< f\left(1-log_2\left(ln2\right)\right)\Rightarrow m\le0\) do m nguyên
Có 20 giá trị nguyên của m