Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
20 tháng 7 2017
y = x – sinx, x ∈ [0; 2 π ].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2 π ]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2 π .
Vậy hàm số đồng biến trên đoạn [0; 2 π ].
PT
1
CM
5 tháng 7 2017
Xét hàm số y = sin(1/x) với x > 0.
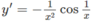
Giải bất phương trình sau trên khoảng (0; + ∞ ):
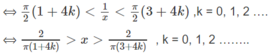
Do đó, hàm số đồng biến trên các khoảng
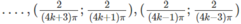
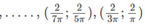
Và nghịch biến trên các khoảng
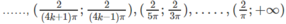
với k = 0, 1, 2 …
P
2
21 tháng 6 2021
kiểu bài này có đáp án trên mạng rồi ấy ạ, anh/chị/ bạn nào mà xem qua đáp án trên mạng có thể giải thích kĩ hơn giúp em chỗ cos 1/x >0 về đoạn sau được không ạ, chứ ai đọc mãi mà không hiểu được 😭😭
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
Bất phương trình lượng giác:
\(cos\left(X\right)\ge a\Leftrightarrow-arccos\left(a\right)+k2\pi\le X\le arccos\left(a\right)+k2\pi\)
Vậy BPT: \(cos\left(\dfrac{1}{x}\right)>0\)
\(\Leftrightarrow-\dfrac{\pi}{2}+k2\pi\le\dfrac{1}{x}\le\dfrac{\pi}{2}+k2\pi\) với \(k\ge1\)
Nghịch đảo: \(\dfrac{2}{k4\pi-\pi}\le x\le\dfrac{2}{k4\pi+\pi}\)
CM
24 tháng 3 2017
Hàm số y = f(x) = -1,5 x 2 có hệ số a = -1,5 < 0 nên hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
24 tháng 2 2021
a) Để hàm số \(y=\left(\sqrt{2n+5}-2\right)x^2\) nghịch biến với mọi x<0 thì
\(\sqrt{2n+5}-2>0\)
\(\Leftrightarrow\sqrt{2n+5}>2\)
\(\Leftrightarrow2n+5>4\)
\(\Leftrightarrow2n>-1\)
\(\Leftrightarrow n>-\dfrac{1}{2}\)
Kết hợp ĐKXĐ, ta được: \(n>-\dfrac{1}{2}\)
Vậy: Để hàm số \(y=\left(\sqrt{2n+5}-2\right)x^2\) nghịch biến với mọi x<0 thì \(n>-\dfrac{1}{2}\)
b) Để hàm số \(y=\left(\sqrt{2n+5}-2\right)x^2\) đồng biến với mọi x<0 thì \(\sqrt{2n+5}-2< 0\)
\(\Leftrightarrow\sqrt{2n+5}< 2\)
\(\Leftrightarrow2n+5< 4\)
\(\Leftrightarrow2n< -1\)
\(\Leftrightarrow n< -\dfrac{1}{2}\)
Kết hợp ĐKXĐ, ta được: \(-\dfrac{5}{2}\le n< \dfrac{1}{2}\)
Vậy: Để hàm số \(y=\left(\sqrt{2n+5}-2\right)x^2\) đồng biến với mọi x<0 thì \(-\dfrac{5}{2}\le n< \dfrac{1}{2}\)
24 tháng 2 2021
a,Nghịch biến khi `x<0`
`<=>\sqrt{2n+5}-2>0(x>=-5/2)`
`<=>\sqrt{2n+5}>2`
`<=>2n+5>4`
`<=>2n> -1`
`<=>n> -1/2`
Kết hợp ĐKXĐ:
`=>n>1/2`
b,Đồng biến với mọi `x<0`
`<=>\sqrt{2n+5}-2<0`
`<=>\sqrt{2n+5}<2`
`<=>2n+5<4`
`<=>2n< -1`
`<=>n< -1/2`
Kết hợp ĐKXĐ:
`=>-5/2<x< -1/2`
22 tháng 7 2021
a) Vì \(3-2\sqrt{2}>0\) nên hàm số đồng biến
b) Thay \(x=3+2\sqrt{2}\) vào hàm số, ta được:
\(y=\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)+\sqrt{2}-1\)
\(=9-8+\sqrt{2}-1\)
\(=\sqrt{2}\)
TA
22 tháng 7 2021
a) `a=3-2\sqrt2>0 =>` Hàm số đồng biến.
b) `y=(3-2\sqrt2)(3+2\sqrt2)+\sqrt2-1=3^2-(2\sqrt2)^2+\sqrt2-1=\sqrt2`
`=> y=\sqrt2` khi `x=3+2\sqrt2`
PT
1
CM
8 tháng 4 2018
TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔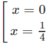 
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng (- ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng (- ∞ ;0 ); (14;+ ∞ )
PT
1
CM
15 tháng 9 2019
TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng (- ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng (- ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
a) y = x – sinx, x ∈ [0; 2π].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2π]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.
Vậy hàm số đồng biến trên đoạn [0; 2π].
c) Xét hàm số y = sin(1/x) với x > 0.
Giải bất phương trình sau trên khoảng (0; + ∞ ):
Do đó, hàm số đồng biến trên các khoảng
Và nghịch biến trên các khoảng
với k = 0, 1, 2 …