Trong không gian Oxyz cho 2 điểm A(3;1;1); B(2;-1;2) và mặt phẳng \(\left(\alpha\right):2x-y-2z+1=0\)
a) Viết phương trình mặt phẳng (P) qua 2 điểm A, B và vuông góc với mặt phẳng\(\left(\alpha\right)\)
b) Viết phương trình mặt cầu (S) tâm A và tiếp xúc với mặt phẳng \(\left(\alpha\right)\)

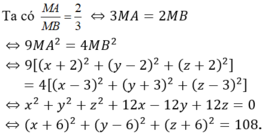

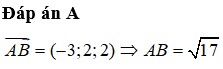
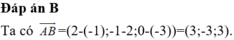


\(\overrightarrow{AB}=\left(-1;-2;1\right)\); \(\overrightarrow{n_{\alpha}}=\left(2;-1;2\right)\)\(\Rightarrow\overrightarrow{n_p}=\left[\overrightarrow{AB};\overrightarrow{n_{\alpha}}\right]=\left(-3;4;5\right)\)
Phương trình mặt phẳng (P) : \(-3x+4y+5z=0\)
\(R=d\left(A;\left(\alpha\right)\right)=\frac{\left|6-1+2+1\right|}{\sqrt{9}}=\frac{8}{3}\)
Phương trình mặt cầu (S) : \(\left(x-3\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=\frac{64}{9}\)