Cho đường thẳng d : 3x-2y+1=0 và M(1;2)
) Viết phương trình qua M và tạo với d một góc 45o. (đừng giải kiểu y=ax+b ạ) giúp emm ạ chi tiết
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thế 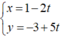 vào phương trình của d’ ta được:
vào phương trình của d’ ta được:
3( 1-2t) -2( -3+5t) -1 =0 hay -16t + 8= 0
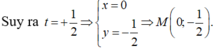
Chọn C.

\(\overrightarrow{AB}=\left(1;2;3\right)\) ; \(\overrightarrow{CD}=\left(1;1;1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{CD}\right]=\left(-1;2;-1\right)=-\left(1;-2;1\right)\)
Phương trình (P):
\(1\left(x-1\right)-2y+1\left(z-1\right)=0\Leftrightarrow x-2y+z-2=0\)
Để tìm phương trình mặt phẳng (P) ta cần tìm được vector pháp tuyến của mặt phẳng. Vì mặt phẳng (P) song song với đường thẳng AB nên vector pháp tuyến của (P) cũng vuông góc với vector chỉ phương của AB, tức là AB(1-0;2-0;4-1)=(1;2;3).
Vì (P) đi qua C(1;0;1) nên ta dễ dàng tìm được phương trình của (P) bằng cách sử dụng công thức phương trình mặt phẳng:
3x - 2y - z + d = 0, trong đó d là vế tự do.
Để tìm d, ta chỉ cần thay vào phương trình trên cặp tọa độ (x;y;z) của điểm C(1;0;1):
3(1) -2(0) - (1) + d = 0
⇒ d = -2
Vậy phương trình của mặt phẳng (P) là:
3x - 2y - z - 2 = 0,
và đáp án là B.

Đáp án: A
Ta có:
(C): x 2 + y 2 - 4x + 2y + 1 = 0 ⇔ (x - 2 ) 2 + (y + 1 ) 2 = 4
⇒ I(2;-1), R = 2
Ta thấy:
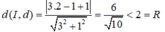
Suy ra, d cắt đường tròn (C) tại hai điểm phân biệt
Thay tọa độ của I vào vế trái phương trình đường thẳng d ta được: 3.2 - 1 + 1 = 6 ≠ 0
Suy ra, I không thuộc d

1: x^2+y^2+6x-2y=0
=>x^2+6x+9+y^2-2y+1=10
=>(x+3)^2+(y-1)^2=10
=>R=căn 10; I(-3;1)
Vì (d1)//(d) nên (d1): x-3y+c=0
Theo đề, ta có: d(I;(d1))=căn 10
=>\(\dfrac{\left|-3\cdot1+1\cdot\left(-3\right)+c\right|}{\sqrt{1^2+\left(-3\right)^2}}=\sqrt{10}\)
=>|c-6|=10
=>c=16 hoặc c=-4
gọi đường thẳng qua M là Δ có vecto n là (a;b) đk a2+b2 ≠ 0
PTTQ của đg đi qua M là a(x-1)+b(y-2)=0 *
ta có CT tính góc giữa hai 2 đt
cos (Δ ;d ) = \(\dfrac{\left|3a-2b\right|}{\sqrt{a^2+b^2}.\sqrt{3^2+\left(-2\right)^2}}=\dfrac{\sqrt{2}}{2}\)
\(2\left|3a-2b\right|=\sqrt{26}\sqrt{a^2+b^2}\)
\(4\left(9a^{2^{ }}+4b-12ab\right)=26\sqrt{a^2+b^2}\)
\(10a^2-48ab-10b^2=0\)
(hd bấm máy tính bạn bấm pt bậc 2 các hệ số lần lượt là a = 10 ,b=-48,c=-10 ra kq là x= 5 và -1:5 ròi ghi a=5b và a=-1:5b nha )
\(\left[{}\begin{matrix}a=5b\\a=-\dfrac{1}{5}b\end{matrix}\right.\)
th1 vs a=5b
chọn b=1 =>a =5 thế vào * => pt đt qua M (ở đây bạn thích chọn b= số nào cx đc nha mình chọn 1 vì tốn giản thôi ở dưới cx tương tự )
th2 vs a=-\(\dfrac{1}{5}\)b
chọn b=-5 => a = 1 thế vào * => pt đt qua M
ôi sai chính tả :< * tối giản