Tìm tập nghiệm S của bất phương trình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)

a, Điều kiện: x > 0
\(log_3\left(x\right)< 2\\ \Rightarrow0< x< 9\)
b, Điều kiện: x > 5
\(log_{\dfrac{1}{4}}\left(x-5\right)\ge-2\\ \Rightarrow x-5\le16\\ \Leftrightarrow5< x\le21\)

\(\log_{\dfrac{1}{4}}x>-2\\ \Rightarrow\left\{{}\begin{matrix}x>0\\\log_{\dfrac{1}{4}}x>\log_{\dfrac{1}{4}}16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>0\\x< 16\end{matrix}\right.\\ \Leftrightarrow0< x< 16\)
Chọn C.

ĐKXĐ: \(x>1\)
\(log_2\left(x-1\right)+log_2\left(x+1\right)=3\)
\(\Leftrightarrow log_2\left(x-1\right)\left(x+1\right)=3\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=8\)
\(\Leftrightarrow x^2-9=0\Rightarrow\left[{}\begin{matrix}x=3\\x=-3< 1\left(l\right)\end{matrix}\right.\)
Vậy tập nghiệm của pt là \(S=\left\{3\right\}\)
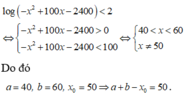
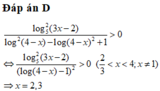
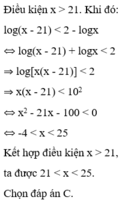
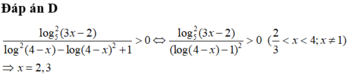


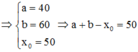
Điều kiện: x > 0
Bất phương trình tương đương với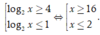
Kết hợp điều kiện ta có S = ( 0 ; 2 ] ∪ [ 16 ; + ∞ ) .
Chọn B.