Giúp mình trình bày rõ cho mình bài tính độ dài vecto này vs!!!
Cho tác giác ABC đều cạnh 6. Tính độ dài vectơ: vtAB+ vtAC ; 1/2 vt AB - 1/4 vt AC
Cho hình chữ nhật cạnh AB= 3a, AD=4a, Xđ các vecto sau rồi tính độ dài vecto:
a, 1/3 vt AB+ 2 vt AD
b, vt AC - vt AD

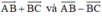
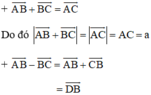
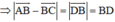
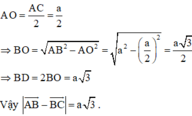
Câu 1:
Gọi M là trung điểm của BC
=>BM=CM=3
\(AM=\sqrt{6^2-3^2}=3\sqrt{3}\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=6\sqrt{3}\)
Câu 2:
b: \(\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{DA}+\overrightarrow{AC}=\overrightarrow{DC}\)
=>|vecto AC-vecto AD|=DC=3a